Khảo sát sự biến thiên và vẽ đồ thị hàm số
Giả sử bạn đang đi ngoài đường. Bạn thấy một người con gái rất xinh. Xẹt! Bạn trúng tia lửa tình. Bạn lân la tìm hiểu, xin inf, facebook, số điện thoại… Tối về bạn nhớ nhung, bạn vẽ ra khuôn mặt hình dáng người con gái ấy. Vâng! Khảo sát sự biến thiên và vẽ đồ thị hàm số cũng như vậy. Bài viết dưới đây sẽ có những thông tin hữu ích cho các bạn về dạng toán này
Content
KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC BA
Hàm số bậc ba (hàm số đa thức bậc 3) là hàm số có dạng y=ax³+bx²+cx+d với a≠0.
Các bước tiến hành bao gồm:
- Nêu tập xác định. Hàm số bậc ba xác định với mọi giá trị của biến x. Do đó tập xác định của nó luôn là R.
- Tính đạo hàm và xét sự biến thiên. Ở bước này thì ta tính đạo hàm của hàm số ta được y’=3ax²+2bx+c. Sau đó tiến hành tìm nghiệm của y’ (nếu có) để xét dấu theo định lý về dấu của tam thức bậc hai. Sau khi xét dấu của y’ ta kết luận về sự biến thiên của hàm số. Đồng thời kết luận luôn về cực trị của hàm số nếu có.
- Giới hạn tại vô cực của hàm số. Đối với hàm số bậc ba ta tính hai giới hạn tại âm vô cực và dương vô cực.
- Lập bảng biến thiên của hàm số. Tất cả thông tin ở bước 2 và 3 sẽ được tổng kết lại trong một bảng biến thiên.
- Tìm tâm đối xứng và giao với các trục tọa độ và vẽ đồ thị. Ở chương trình sách giáo khoa hiện nay đã tinh giản phần tính lồi lõm của hàm số. Vì vậy để vẽ được đồ thị hàm số bậc ba thì ta tìm tâm đối xứng và các giao điểm với các trục (nếu có) hoặc lấy thêm 1 đến 2 điểm để vẽ đồ thị hàm số. Để tìm tâm đối xứng ta tìm nghiệm của phương trình y”=0. Đó chính là hoành độ tâm đối xứng. Tung độ tâm đối xứng là giá trị của hàm số tại hoành độ tâm đối xứng.
- Vẽ đồ thị hàm số. Để vẽ đồ thị hàm số ta dựa vào hình dáng 6 dạng đồ thị đã được phác thảo trong sách giáo khoa nhé.
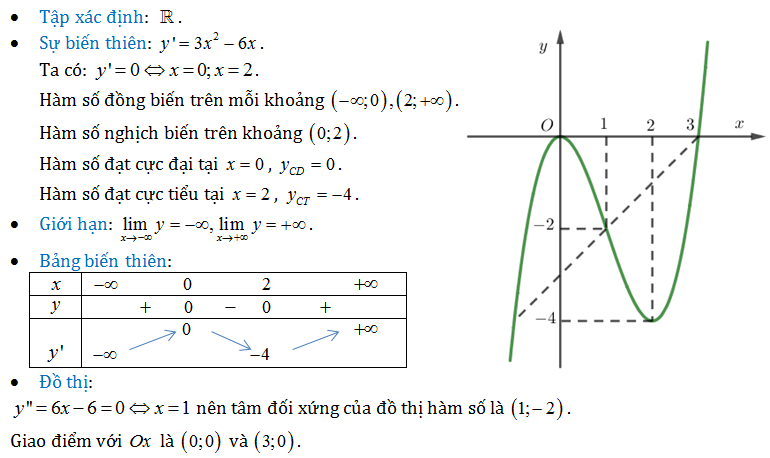
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số y=x³-3x².
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC BỐN
Hàm số bậc bốn (hàm số đa thức bậc 4 trùng phương) là hàm số có dạng với a≠0.
Các bước tiến hành bao gồm:
- Nêu tập xác định. Hàm số bậc bốn xác định với mọi giá trị của biến x. Do đó tập xác định của nó luôn là R.
- Tính đạo hàm và xét sự biến thiên. Ở bước này thì ta tính đạo hàm của hàm số ta được y’=4ax³+2bx=2x(ax²+b). Sau đó tiến hành tìm nghiệm của y’ để xét dấu. Lưu ý là y’ luôn đan dấu qua các nghiệm. Sau khi xét dấu của y’ ta kết luận về sự biến thiên của hàm số. Đồng thời kết luận luôn về cực trị của hàm số (hàm bậc bốn luôn có ít nhất 1 điểm cực trị).
- Giới hạn tại vô cực của hàm số. Đối với hàm số bậc bốn ta tính hai giới hạn tại âm vô cực và dương vô cực.
- Lập bảng biến thiên của hàm số giống như với hàm số bậc 3.
- Vẽ đồ thị hàm số. Đồ thị hàm số bậc 4 nhận trục Oy là trục đối xứng.
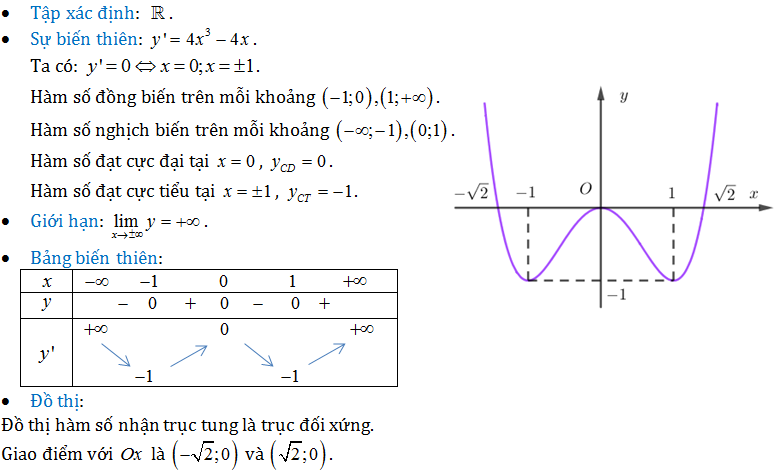
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ TΗỊ HÀM SỐ PHÂN TUYẾN TÍNH
Hàm số phân tuyến tính là hàm số có dạng .
Hàm số này còn được gọi là hàm số phân thức bậc nhất trên bậc nhất. Một số người gọi hàm số này là hàm “nhất biến”. Tôi thì không ưa cái tên “nhất biến” này lắm.
Theo tôi, đây là hàm số dễ khảo sát và vẽ đồ thị nhất vì nó có 1 form khá đơn giản.
- Nêu tập xác định. Hàm phân tuyến tính xác định khi mẫu số khác 0.
- Tính đạo hàm và xét sự biến thiên. Đạo hàm của hàm số có cách tính nhanh theo công thức:
- Giới hạn của hàm số. Ta tính giới hạn của hàm số tại vô cực suy ra được đường tiệm cận ngang. Tính giới hạn một bên tại điểm triệt tiêu của mẫu được tiệm cận đứng.
- Lập bảng biến thiên của hàm số.
- Vẽ đồ thị hàm số. Đồ thị hàm số phân tuyến tính có tâm đối xứng chính là giao điểm của hai đường tiệm cận.
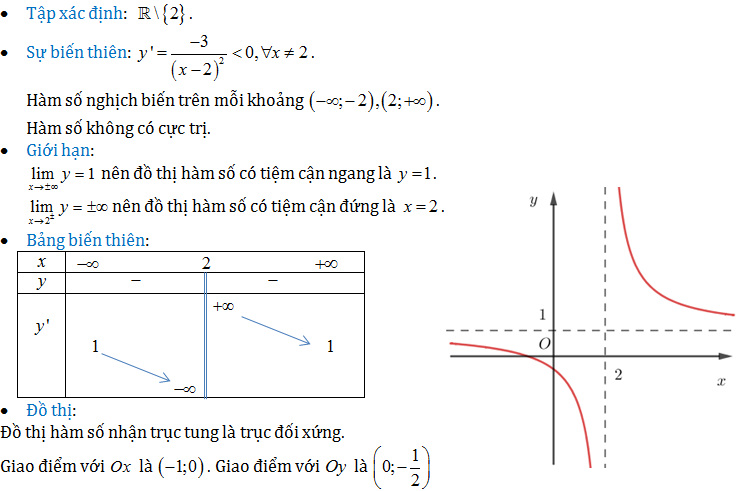
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số .
Trên đây là cách giải bài toán khảo sát hàm số của 3 loại hàm số trong chương trình THPT. Trong khuôn khổ 1 bài viết chưa thể đầy đủ hết được các tình huống. Nhưng chắc chắn là một gợi ý tốt cho các bạn nghiên cứu và tự học. Chúc các bạn thành công!
Xem thêm:
Dạng toán nhận dạng đồ thị hàm số lớp 12
Hàm số -Tìm cực trị của hàm số chứa trị tuyệt đối
Khảo sát hàm số bậc 3 và đánh giá hệ số hàm số bậc 3
Bài tập trắc nghiệm nhận dạng đồ thị hàm số
Sử dụng tính đơn điệu của hàm số để giải phương trình
Bài tập trắc nghiệm tính đơn điệu của hàm số
Tìm cực trị của hàm số như thế nào ?
Tâm đối xứng của đồ thị hàm số bậc 3