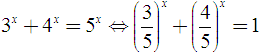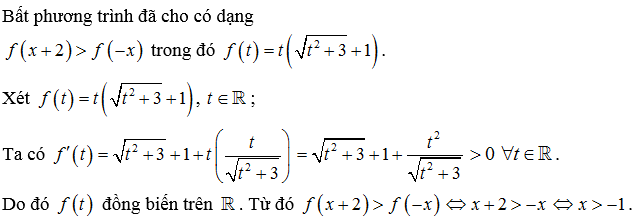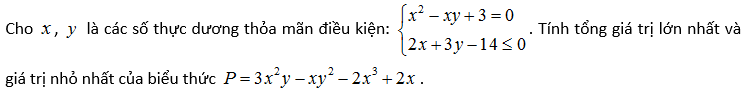Sử dụng tính đơn điệu của hàm số để giải phương trình
Sử dụng tính đơn điệu của hàm số để giải phương trình là một trong các phương pháp để giải phương trình. Đây là một trong các phương pháp giải phương trình, bất phương trình hay hệ phương trình mà tôi sẽ giới thiệu đến các bạn trong bài viết này. Cụ thể như thế nào chúng ta hãy cùng theo dõi nhé.
I. SỬ DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ĐỂ GIẢI PHƯƠNG TRÌNH
Ứng dụng tính đơn điệu của hàm số vào giải phương trình có nhiều dạng, nhiều cách hỏi. Tuy nhiên điểm mấu chốt trong đó là ta khai thác tính chất: Nếu hàm số f(x) đơn điệu tăng trong khoảng (a;b) và hàm số g(x) đơn điệu giảm trên khoảng (a;b). Thì nếu phương trình f(x)=g(x) có nghiệm thì đó là nghiệm duy nhất. Nếu 1 trong 2 hàm số f(x) hoặc g(x) là hàm hằng. Hàm còn lại đơn điệu. Thì tính chất trên vẫn đúng.
Ví dụ 1:
Cho phương trình
Giải phương trình bằng phương pháp hàm số.
Lời giải:
Trước hết ta biến đổi phương trình đã cho.
Hàm số vế trái là hàm số đơn điệu giảm. Hàm số ở vế phải là hàm hằng. Mặt khác ta nhẩm được nghiệm của phương trình là x=2. Vậy phương trình đã cho có nghiệm duy nhất x=2.
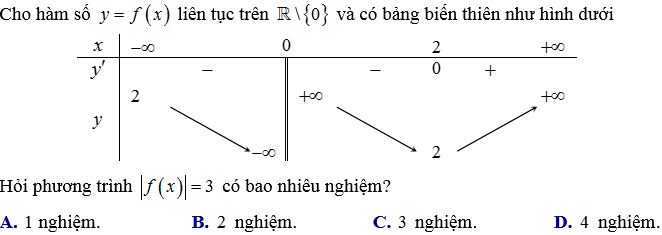
Ví dụ 2: (Nguồn THTT)
Lời giải:
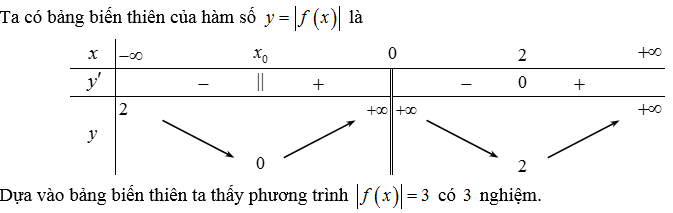
Theo giả thiết ta thấy có thể lập bảng biến thiên của hàm |f(x)|. Sau đó sử dụng tính đơn điệu của hàm số |f(x)| để kết luận số nghiệm của phương trình đã cho.
Cách xác định bảng biến thiên của hàm |f(x)| từ bảng biến thiên hàm f(x) là:
Lấy đối xứng phần âm (bên dưới trục Ox) qua trục Ox. Sau đó bỏ phần bên dưới trục Ox.
Ở bài này ta thấy nhánh bên trái cắt trục Ox tai điểm x_{0} nào đó. Còn nhánh bên phải không có phần âm nên giữ nguyên.
Từ đó ta chọn được đáp án C.
Ví dụ 3:
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
II. SỬ DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ĐỂ GIẢI HỆ PHƯƠΝG TRÌNH
Về cơ bản thì nguyên tắc áp dụng phương pháp này không có gì thay đổi. Chỉ có điều việc biến đổi sẽ phức tạp hơn nếu giả thiết bài toán cho bởi hệ phương trình,
Ví dụ 4:
Lời giải:
Trên đây là gợi ý về cách ứng dụng tính đơn điệu của hàm số để giải phương trình hệ phương trình. Các bạn hãy luyện tập thêm về dạng toán này nhé. Chúc các bạn thành công!
Xem thêm: Cách xét tính đơn điệu của hàm số
Hàm số -