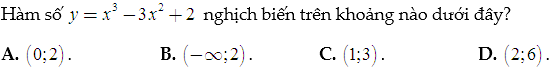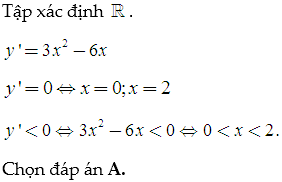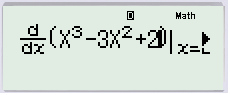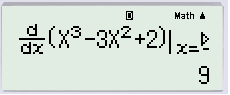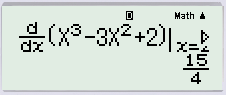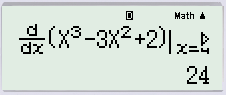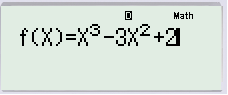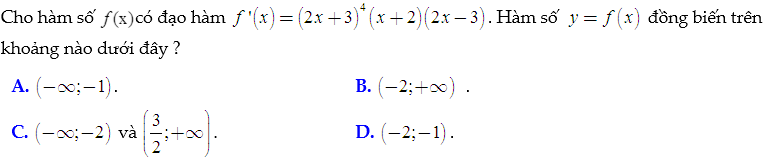Bài tập trắc nghiệm tính đơn điệu của hàm số
Bài tập trắc nghiệm tính đơn điệu của hàm số full dạng và cách giải cập nhật thường xuyên. Trắc nghiệm tính đơn điệu của hàm số rất đa dạng và phong phú. Vì vậy ta phân loại thành các dạng bài tập trắc nghiệm về tính đơn điệu của hàm số. Như vây sẽ giúp các em học và phản ứng nhanh hơn với loại toán này. Cùng theo dõi và lấy giấy bút làm theo các ví dụ nào!
Content
- 1 CÁC DẠNG BÀI TẬP TRẮC NGHIỆM TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
- 1.1 Dạng 1. Cho hàm số y=f(x), tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
- 1.2 Dạng 2. Cho đồ thị hàm số y=f(x), tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
- 1.3 Bài tập trắc nghiệm tính đơn điệu của hàm số Dạng 3. Hàm số y=f(x) cho trước y=f'(x), tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
- 1.4 Dạng 4. Hàm số y=f(x) cho bởi bảng biến thiên, tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
CÁC DẠNG BÀI TẬP TRẮC NGHIỆM TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Dạng 1. Cho hàm số y=f(x), tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
Với dạng này thì f(x) đã biết, nên chúng ta chỉ cần xét dấu đạo hàm để tìm khoảng đơn điệu. Chúng ta cũng có thể dùng phương pháp loại trừ hoặc máy tính bỏ túi để giải trắc nghiệm.
Ví dụ:
Lời giải:
Cách 1. Xét dấu đạo hàm
Cách 2. Phương pháp loại trừ kết hợp máy tính bỏ túi
Dùng chức năng d/dx để tính đạo hàm của hàm số tại các điểm cụ thể.
Vì x=−1 có trong phương án B nhưng không có trong phương án A. Nên để loại phương án A hoặc B ta chọn x=−1.
Ta được kết quả là 9 nên ta loại phương án B.
Vì x=2,5 có trong phương án C nhưng không có trong phương án A. Nên ta tiếp tục chọn x=2,5. (Lưu ý chỉnh sửa trên công thức lúc nãy chứ không phải bấm lại từ đầu).
Ta được kết quả là 15/4 nên ta loại phương án C.
Vì x=4 có trong phương án D nhưng không có trong phương án A nên ta chọn x=4.
Ta được kết quả là 24 nên ta loại phương án D.
Từ đó ta chọn được đáp án là A.
Cách này giải thích thì dài dòng nhưng khi thực hiện thì rất nhanh. Tuy nhiên việc chọn giá trị đôi khi lại không ” thuận buồm xuôi gió” như ví dụ đâu nhé. Hãy hiểu bản chất trước khi lao đầu vào bấm máy tính.
Cách 3. Dùng chức năng TABLE trong máy tính bỏ túi
Chúng ta vào chức năng MODE 7 chế độ 1 hàm số và nhập hàm số.
START chọn −2, END chọn 6, STEP chọn 0.5 (Việc lựa chọn căn cứ vào các khoảng trong 4 phương án).
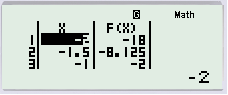
Sau đó ta xem xét sự tăng giảm giá trị ở cột F(X). Nếu tăng là dấu hiệu đồng biến, giảm thì ngược lại. Từ đó ta chọn được đáp án A.
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
Dạng 2. Cho đồ thị hàm số y=f(x), tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
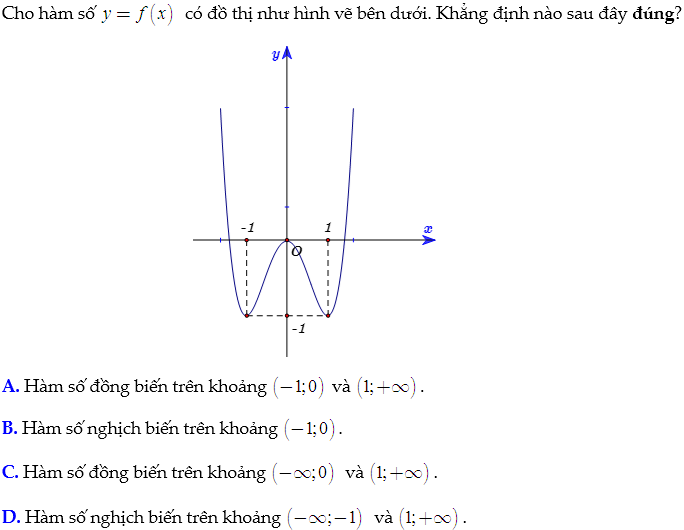
Dạng này khác dạng 1 ở cách cho hàm số. Ở đây hàm số được cho bởi 1 phần của đồ thị. Đây thường là câu hỏi nhận biết bởi vì chúng ta có thể dựa vào hình dáng đồ thị để nhận xét về sự đơn điệu. Nếu tính từ trái qua phải đồ thị có dáng “đi lên” thì hàm số đồng biến và ngược lại nếu “đi xuống” thì là nghịch biến.
Ví dụ: (Nguồn Strong Team VD VDC)
Lời giải:
Dựa vào đồ thị hàm số ta loại phương án D vì trên khoảng (1;+∞) đồ thị hàm số không “hoàn toàn đi xuống”.
Tương tự ta loại phương án C vì trên khoảng (−∞;0) đồ thị hàm số không “hoàn toàn đi lên”.
Phương án A và B mới nhìn thì có vẻ đều hợp lý. Nhưng chúng ta để ý thì đây chỉ là một phần đồ thị hàm số nên ta không thể khẳng định được hàm số đồng biến trên (1;+∞).
Đáp án của bài toán là A.
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
Bài tập trắc nghiệm tính đơn điệu của hàm số
Dạng 3. Hàm số y=f(x) cho trước y=f'(x), tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
Dạng này chúng ta nên giải phương trình f'(x)=0 và xét dấu f'(x). Nên xét theo bội của nghiệm sẽ nhanh hơn.
Ví dụ:
Lời giải:
Hàm số f'(x) có 3 nghiệm là −2 (nghiệm đơn); −3/2 (nghiệm bội 4); 3/2 (nghiệm đơn) và f'(+∞)>0. Nên xét dấu f'(x) ta được:
Chú ý là qua nghiệm bội chẵn (-3/2) f'(x) không đổi dấu.
Từ đó ta chọn được đáp án C.
Dạng 4. Hàm số y=f(x) cho bởi bảng biến thiên, tìm khoảng đồng biến hoặc nghịch biến của hàm số f(x)
(Đang cập nhật)
Hàm số -