Bài tập trắc nghiệm nhận dạng đồ thị hàm số

Nhận dạng đồ thị hàm số là một dạng toán thường thấy trong các đề thi trắc nghiệm toán. Bài viết dưới đây tôi sẽ tổng hợp các dạng bài tập trắc nghiệm nhận dạng đồ thị hàm số và phương pháp giải. Theo dõi bài viết để học tập và tìm hiểu thêm nhé!

Content

BÀI TẬP TRẮC NGHIỆM NHẬN DẠNG ĐỒ THỊ HÀM SỐ

LOẠI 1. CHO ĐỒ THỊ- HỎI ĐỒ THỊ ĐÓ CỦA HÀM SỐ NÀO?

Để nhận dạng đồ thị hàm số, chúng ta cần chú ý đến các yếu tố có trên đồ thị hàm số như: Hình dáng đồ thị;Giao điểm với các trục Ox, Oy; Điểm; Sự biến thiên; Cực trị. Đây xũng là thứ tự ưu tiên của các yếu tố khi ta làm dạng toán nhận dạng đồ thị hàm số. Phương pháp chủ đạo đối với dạng toán này theo tôi là phương pháp loại trừ. Sau đây chúng ta cùng tìm hiểu các dạng toán thông qua các bài toán cụ thể.

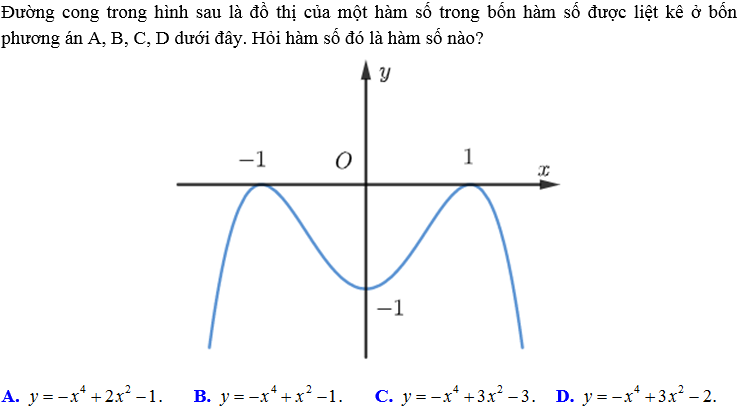
Bài 1:

trắc nghiệm nhận dạng đồ thị hàm số

Hướng dẫn:

Dựa vào hình dáng đồ thị ta không loại được phương án nào.

Ta thấy trên đồ thị có điểm (0;-1) giúp ta loại được phương án C và D. Điểm (1;0) giúp ta loại được phương án B.

Vậy ta chọn được đáp án A.

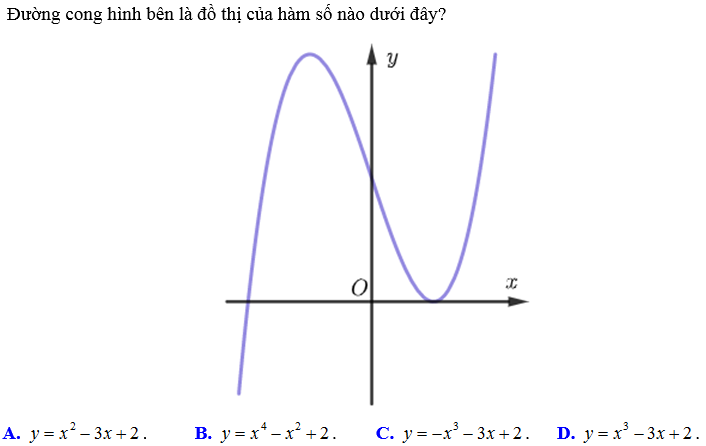
Bài 2:

trắc nghiệm đồ thị hàm số

Hướng dẫn:

Chỉ dựa vào hình dáng đồ thị ta có thể loại được phương án A, B và C. Vậy đáp án là D.

Qua 2 bài này ta có thể rút ra nhận xét: Càng ít số liệu trên đồ thị thì dáng điệu đồ thị càng quan trọng. Tuy nhiên hãy tỉnh táo với bài dưới đây.

Đề thi Online có giải: [5-6] Nhận dạng hàm số thường gặp thông qua đồ thị

Bộ đề thi Online các dạng có giải chi tiết: Hàm số

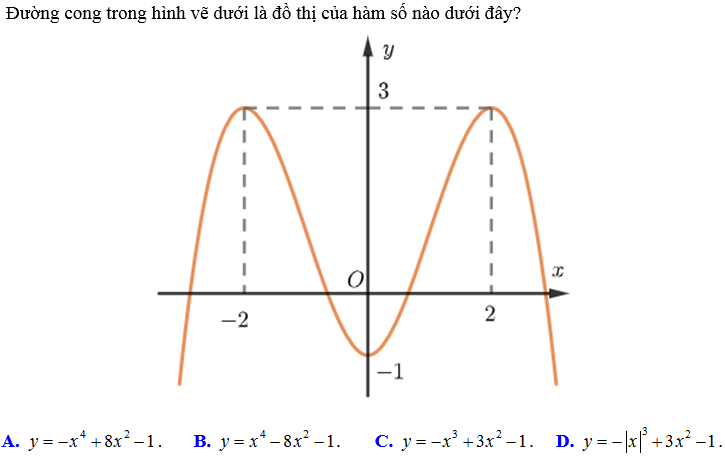
Bài 3:

Hướng dẫn:

Dựa vào dáng điệu đồ thị hàm số ta có thể loại ngay được phương án B và C.

Thay điểm (2;3) ta loại được phương án A. Vậy đáp án là D.

LOẠI 2. CHO ĐỒ THỊ – HỎI DẤU HOẶC SO SÁNH CÁC HỆ SỐ CỦA HÀM SỐ

Với loại nay chúng ta thường phải vận dụng nhiều kiến thức hơn so với dạng 1. Tùy từng bài toán các bạn hãy vận dụng các tính chất phù hợp vào giải toán.

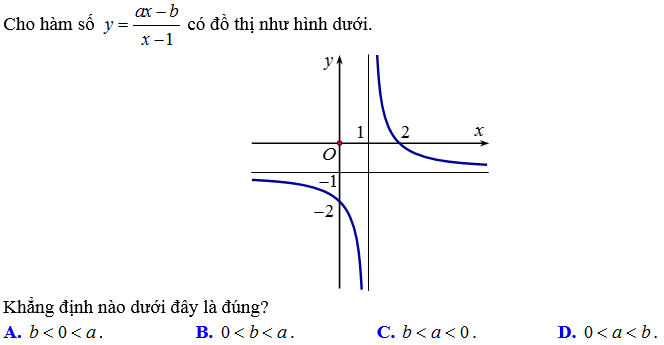
Bài 1:

Hướng dẫn:

Đồ thị hàm số có tiệm cận ngang y=a nên a=-1.

Tung độ giao điểm của đồ thị hàm số với trục Oy là b nên b=-2.

Vậy đáp án là C.

Bài 2:

Đề thi Online có giải: [7-8] Xét dấu của các hệ số hàm số thông qua đồ thị

Bộ đề thi Online các dạng có giải chi tiết: Hàm số

Hướng dẫn:

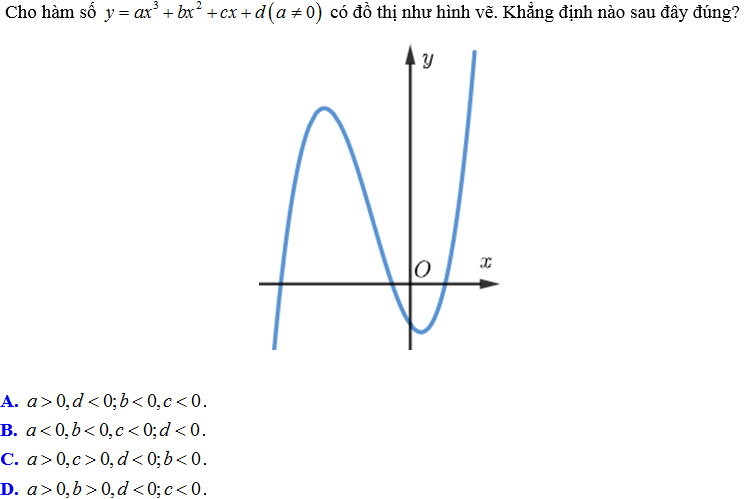
Dựa vào dáng điệu đồ thị hàm số suy ra a dương. Do đó ta loại được phương án B.

Hàm số có 2 điểm cực trị trái dấu nên a và c trái dấu. Do đó c âm. Ta loại được phương án C.

Hoành độ tâm đối xứng âm nên a và b cung dấu. Do đó b dương. Ta loại được phương án A và chọn được đáp án D.

Trên đây là 1 số ví dụ về dạng toán nhận dạng đồ thị hàm số và gợi ý cách làm dạng toán này. Chúc các bạn học giỏi và thành công!

Hàm số -