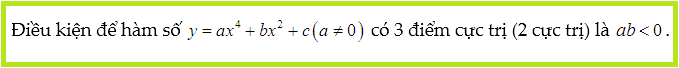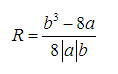Tìm m để hàm số có 3 cực trị (hàm số trùng phương)
Tìm m để hàm số có 3 cực trị của hàm số trùng phương bậc 4. Đây là một trong các dạng toán về cực trị của hàm số trùng phương bậc 4. Bài viết sẽ hướng dẫn các bạn cách tìm m để hàm trùng phương có 3 điểm cực trị. Đồng thời bài viết cũng hướng dẫn 1 số dạng toán khác về cực trị của hàm số trùng phương. Bắt đầu nào!
Content
TÌM M ĐỂ HÀM SỐ CÓ 3 ĐIỂM CỰC TRỊ
Trước hết chúng ta cần giải thích 1 chút về từ ngữ. Ở đầu bài viết có viết “tìm m để hàm số có ba cực trị”. Viết như vậy không được chính xác với khái niệm của SGK. Vì điểm cực trị của hàm số khác với cực trị của hàm số. Chính xác thì hàm trùng phương bậc 4 chỉ có tối đa 2 cực trị. Và bài toán phải phát biểu lại là “tìm m để hàm số có ba điểm cực trị (hoặc 2 cực trị)”. Sau đây là điều kiện để hàm số trùng phương có 2 cực trị:
Ví dụ:
Cho hàm số
Tìm tất cả các giá trị của m để hàm số đã cho có ba điểm cực trị.
Lời giải:
Ba điểm cực trị của đồ thị hàm số trùng phương bậc 4 (nếu có) luôn tạo thành tam giác cân. Vì vậy bài toán thường được hỏi thêm điều kiện ba điểm cực trị tạo thành: Tam giác đều; Tam giác vuông; Tam giác có góc 120°; Bán kính đường tròn ngoại tiếp…
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
BA ĐIỂM CỰC TRỊ TẠO THÀNH TAM GIÁC ĐỀU
Ví dụ:
Cho hàm số
Tìm m để đồ thị hàm số đã cho có ba điểm cực trị tạo thành một tam giác đều.
Lời giải:
BA ĐIỂM CỰC TRỊ TẠO THÀNH TAM GIÁC CÓ BÁN KÍNH ĐƯỜNG TRÒN NGOẠI TIẾP BẰNG R
Công thức tính bán kính đường tròn ngoại tiếp tam giác có 3 đỉnh là ba cực trị hàm trùng phương:
Đề thi Online có giải: [7-8] Tìm m để hàm số có 3 cực trị
Chúc các bạn thành công!
Hàm số -