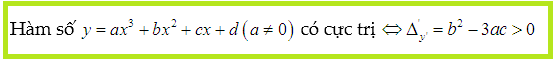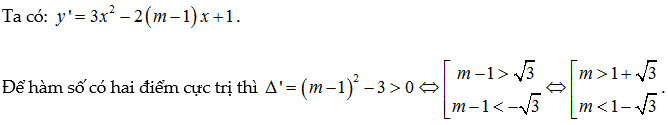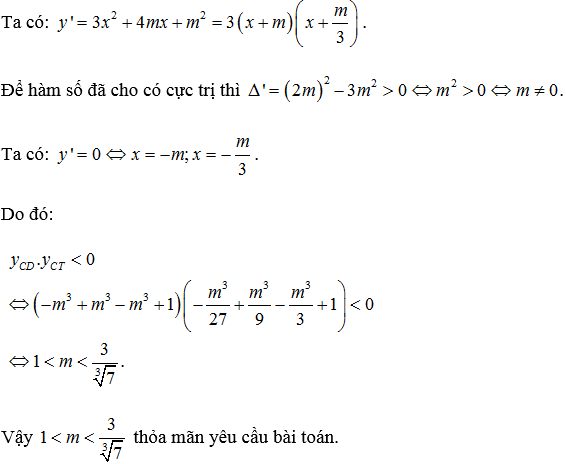Tìm m để hàm số có cực trị (hàm số đa thức bậc 3)
Tìm m để hàm số có cực trị. Đây là 1 trong các dạng toán về cực trị của hàm số đa thức bậc 3 y=ax³+bx²+cx+d (a≠0). Bài viết dưới đây sẽ giới thiệu và hướng dẫn cách giải các dạng toán tìm m để hàm đa thức bậc ba có cực trị thỏa mãn điều kiện cho trước. Bắt đầu nào!
Content
TÌM M ĐỂ HÀM SỐ ĐA THỨC BẬC 3 CÓ 2 CỰC TRỊ
Hàm số đa thức bậc ba có cực trị thì sẽ có đúng hai cực trị. Trong đó có 1 cực đại và một cực tiểu.
Ví dụ:
Cho hàm số y=x³-(m-1)x²+x+2020. Tìm m để hàm đã cho có 2 cực trị.
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
TÌM M ĐỂ HÀΜ SỐ ĐA THỨC BẬC 3 CÓ 2 CỰC TRỊ TRÁI DẤU
Dạng toán này tương đương với dạng toán tìm m để đồ thị hàm đa thức bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành.
Ví dụ:
Cho hàm số y=x³+2mx²+m²x+1 (C). Tìm m để (C) có 2 điểm cực trị nằm về hai phía của trục hoành.
Lời giải:
Lưu ý: Trước hết chúng ta cần tìm điều kiện để hàm số có cực trị đã.
Đề thi Online có giải: [7-8 Điểm] Tìm m để hàm số bậc 3 có cực trị thỏa mãn điều kiện cho trước
TÌM M ĐỂ HÀΜ SỐ ĐA THỨC BẬC 3 CÓ 2 ĐIỂM CỰC TRỊ TRÁI DẤU
Dạng toán này tương đương với dạng toán tìm m để đồ thị hàm đa thức bậc 3 có 2 điểm cực trị nằm về 2 phía trục tung.
Ví dụ:
Lời giải:
tìm m để hàm số có cực đại
tìm điều kiện để hàm số có cực trị
tìm m để hàm số có cực trị trên khoảng
Hàm số -