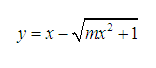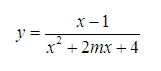Tìm m để hàm số có tiệm cận ngang tiệm cận đứng

Tìm m để hàm số có tiệm cận ngang tiệm cận đứng là một trong các dạng toán về đường tiệm cận. Bài viết dưới đây sẽ hướng dẫn các em học sinh cách làm dạng toán này.

TÌM M ĐỂ HÀM SỐ CÓ TIỆM CẬN NGANG

Hàm số y=f(x) muốn có tiệm cận ngang thì cần thỏa mãn đủ các điều kiện sau:

+Tập xác định có chứa các điểm vô cực. Tức là tập xác định của hàm số cần có các tập con có dạng (a;+∞) hoặc (−∞;a).

+Một trong các giới hạn của hàm số f(x) khi x tiến tới âm vô cực hoặc dương vô cực phải là giá trị hữu hạn.

Vì vậy với các bài toán tìm điều kiện của m để hàm số có tιệm cận ngang ta cần tìm m thỏa mãn các điều kiện nêu trên.

Ví dụ:

Tìm m để hàm sau có tiệm cận ngang:

Lời giải:

Trước hết điều kiện xác định của hàm số là mx²+1≥0. Vì vậy muốn tập xác định chứa vô cực thì m≥0.

Đề thi Online có giải: [7-8] Định m để đồ thị hàm số có đường tiệm cận thỏa mãn điều kiện cho trước

Bộ đề thi Online các dạng có giải chi tiết: Tiệm cận Hàm số

TÌM M ĐỂ HÀM SỐ CÓ TIỆM CẬN ĐỨNG

Hàm số y=f(x) muốn có tiệm cận đứng thì cần thỏa mãn đủ các điều kiện sau:

+Có các điểm mà hàm số không xác định. Đồng thời tồn tại lân cận trái hoặc phải của điểm đó là tập con của tập xác định của hàm số f(x).

+Tồn tại ít nhất 1 giới hạn một bên tại các điểm nêu trên bằng vô cực.

Với bài toán tìm m để đồ thị hàm số có đường tiệm cận đứng ta cần tìm m thỏa mãn các điều kiện trên. Đối với hàm số phân thức thường chúng ta sẽ tìm điều kiện để mẫu có nghiệm và nghiệm của mẫu không là nghiệm của tử số.

Ví dụ:

Cho hàm số