Đồ thị hàm số và một số dạng toán thường gặp
Đồ thị hàm số là gì? Một vài dạng toán thường gặp trong chương trình THPT, THCS về đồ thị hàm sẽ được đề cập trong bài viết này một cách tổng quát. Bài viết chi tiết hơn sẽ có ở cuối bài viết này.
Content
ĐỊNH NGHĨA ĐỒ THỊ HÀM SỐ
Cho hàm số y=f(x) xác định trên khoảng K. Quỹ tích các điểm M(x;f(x)) với x thuộc K được gọi là đồ thị của hàm số y=f(x). Đồ thị hàm trong chương trình toán THPT được biểu diễn trên mặt phẳng tọa độ Descartes vuông góc. Như vậy đồ thị của hàm là một biểu diễn trực quan về sự biến thiên, cực trị, tâm đối xứng, trục đối xứng, chu kỳ … của hàm đó.
Đồ thị của hàm số
MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
DẠNG 1: VẼ ĐỒ THỊ HÀM SỐ
Đây là một dạng toán thường gặp xuất hiện từ lớp 7 và trải dài đến lớp 12. Tuy nhiên chúng ta chỉ cần tập trung vào một số dạng hàm số cụ thể: Hàm số bậc nhất y=ax+b (lớp 7→lớp 10), hàm số bậc hai y=ax²+bx+c (lớp 9→10), hàm số đa thức bậc ba, hàm số đa thức bậc 4 trùng phương, hàm số phân thức bậc nhất trên bậc nhất ( lớp 12). Còn đối với hàm số lượng giác (lớp 11), hàm số lũy thữa, mũ, logarit (lớp 12) chúng ta chỉ cần nắm được các tính chất để hỗ trợ các dạng toán khác.
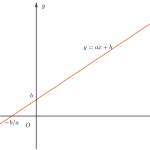
VẼ ĐỒ THỊ HÀM SỐ BẬC NHẤT
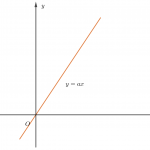
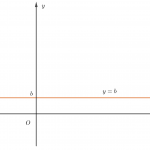
Đồ thị hàm số bậc nhất y=ax+b là một đường thẳng và xuất hiện từ các bài toán đồ thị hàm số lớp 7. Để vẽ dđồ thị hàm số bậc nhất người ta thường lấy hai điểm bất kỳ trên đường thẳng đó. Tuy nhiên để dễ dàng trong tính toán người ta thường lấy giao điểm của đường thẳng với các trục tọa độ. Trong trường hợp b=0 đường thẳng y=ax+b đi qua gốc tọa độ. Khi đó ta lấy thêm điểm (1;a) bằng cách cho x=1 suy ra y=a chẳng hạn. Trường hợp a=0 thì đường thẳng đi qua điểm (0;b) và song song với trục hoành.
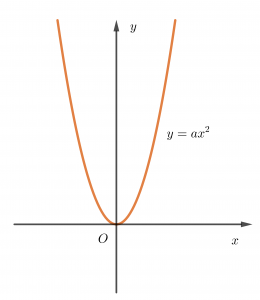
VẼ ĐỒ THỊ HÀM SỐ BẬC HAI
Đồ thị hàm bậc hai y=ax²+bx+c (a≠0) là một đường Parabol có trục đối xứng là x=-b/2a và tung độ đỉnh là -Delta/4a. Cách vẽ Parabol chúng ta thực hiện lần lượt các bước sau: Vẽ trục đối xứng, đỉnh, lấy thêm 1 đến 2 điểm. Đồ thị hàm số bậc 2 có từ các bài toán về đồ thị hàm số lớp 9. Tuy nhiên ở lớp 9 thì chúng ta chỉ mới xét đến đồ thị hàm y=ax² mà thôi.
VẼ ĐỒ THỊ HÀM SỐ LỚP 12
Đến lớp 12 với các công cụ mạnh mẽ là đạo hàm ta mới có thể vẽ được đồ thi các hàm đa thức bậc ba, hàm đa thức trùng phương bậc 4, hàm phân thức bậc nhất trên bậc nhất. Để vẽ được đồ thị các hàm này ta sử dụng đạo hàm để khảo sát hàm và xét sự biến thiên. Dựa vào đó ta có thể vẽ được đồ thị.
Cách khảo sát và vẽ đồ thị hàm số lớp 12 (cách khảo sát đồ thị hàm số) cơ bản gồm các bước như: Tập xác định→Đạo hàm→Xét sự biến thiên→Giới hạn→Tiệm cận→Cực trị→Đdồ thị. Cách khảo sát hàm số có thể thay đổi ở một vài nội dung với từng hàm số cụ thể.
Khảo sát vẽ đồ thị hàm là dạng toán “gỡ điểm” khi còn thi tốt nghiệp, đại học dưới hình thức tự luận.
Hiện nay câu hỏi trong các kỳ thi bằng hình thức trắc nghiệm. Nên bài toán về các dạng khảo sát hàm số và vẽ đồ thị được tách nhỏ thành các câu hỏi. Chẳng hạn như 1 câu chỉ hỏi về sự biến thiên còn câu khác lại hỏi về đồ thị.
DẠNG 2: BÀI TOÁN TƯƠNG GIAO
Một phương trình f(x)=g(x) có thể xét dưới góc độ là tương giao của đồ thị hai hàm y=f(x) và y=g(x). Số nghiệm của phương trình cũng là số giao điểm của hai đồ thị. Đồng thời hoành độ giao điểm cũng là nghiệm của phương trình. Việc xét tương giao như vậy rất thuận tiện trong các bài toán mà đồ thị dễ dựng hoặc đã có sẵn.
Ví dụ:
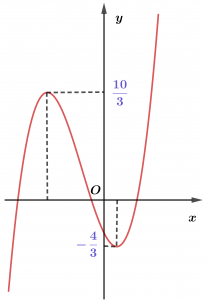
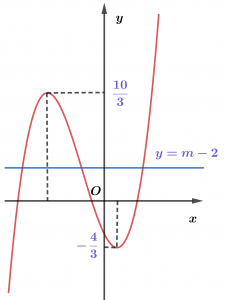
Hình bên là đồ thị hàm y=ax³+bx²+cx+d.
Tìm m để phương trình ax³+bx²+cx+d=m-2 có ba nghiệm phân biệt.
Lời giải:
Nghiệm của phương trình ax³+bx²+cx+d=m-2 là hoành độ giao điểm của đồ thị hàm y=ax³+bx²+cx+d và đường thẳng y=m-2.
Dựa vào đồ thị đã cho suy ra phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi: -4/3<m-2<10/3 ⇔2/3<m<16/3.
DẠNG 3. NHẬN DẠNG ĐỒ THỊ HÀM SỐ
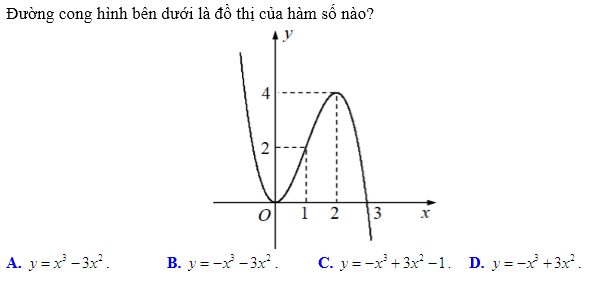
Đây là một dạng toán mới có nhiều lên kể từ khi có thi trắc nghiệm toán. Thường đây là một bài toán chỉ ở mức độ nhận biết (mức 1). Hình thức cho thường là cho đồ thị một hàm nào đó. Sau đó yêu cầu chúng ta phải tìm được hàm nào trong các phương án có đồ thị như vậy. Để làm tốt dạng toán này thì chúng ta cần phải nhớ được tính chất của đồ thị từng loại hàm như đã nói ở dạng 1.
Ví dụ:
Lời giải:
Dựa vào “dáng điệu” đồ thị và các phương án ta suy ra đây là đồ thị một hàm đa thức bậc ba y=ax³+bx²+cx+d có a âm. Loại được phương án A.
Dựa vào giao điểm với trục tung là O(0;0) ta loại được phương án C.
Thay tọa độ điểm (1;2) vào hai phương án B, D ta loại được phương án B.
Vậy ta chọn phương án D là đáp án.
Xem thêm:
- Hàm số lượng giác – Dạng bài tập và phương pháp giải
- Cách vẽ đồ thị hàm số bậc 2 ở lớp 10
- Hàm số bậc nhất – Dạng bài tập thường gặp
- Đồ thị hàm số bậc 4 và một số dạng toán thường gặp
- Phương trình tiếp tuyến của đồ thị hàm số
- Tập xác định của hàm số mũ lũy thừa lôgarit
- Hàm số chẵn lẻ, cách xét tính chẵn lẻ của hàm số
- Tìm tập xác định của hàm số ở lớp 10
- Giới hạn hàm số – Cách xử lý các dạng vô định
Blog Toán Học -