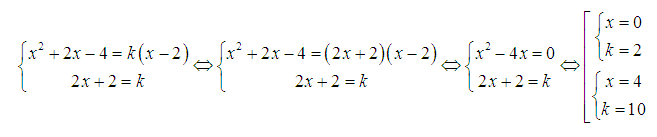Phương trình tiếp tuyến của đồ thị hàm số

Phương trình tiếp tuyến của đồ thị hàm số viết như thế nào? Bài viết dưới đây sẽ hướng dẫn các em học sinh cách viết phương trình tiếp tuyến từ dạng dễ đến dạng khó. Các em cùng theo dõi nhé!.

Content

ĐƯỜNG TIẾP TUYẾN ĐỒ THỊ HÀM SỐ

Cho hàm số y=f(x) có đồ thị là đường cong (C). Cho điểm M và N nằm trên (C). Khi điểm M và N gần nhau vô hạn thì đường thẳng MN được gọi là 1 tiếp tuyến của (C) tại M ( hoặc N) (Theo Leibniz).

 

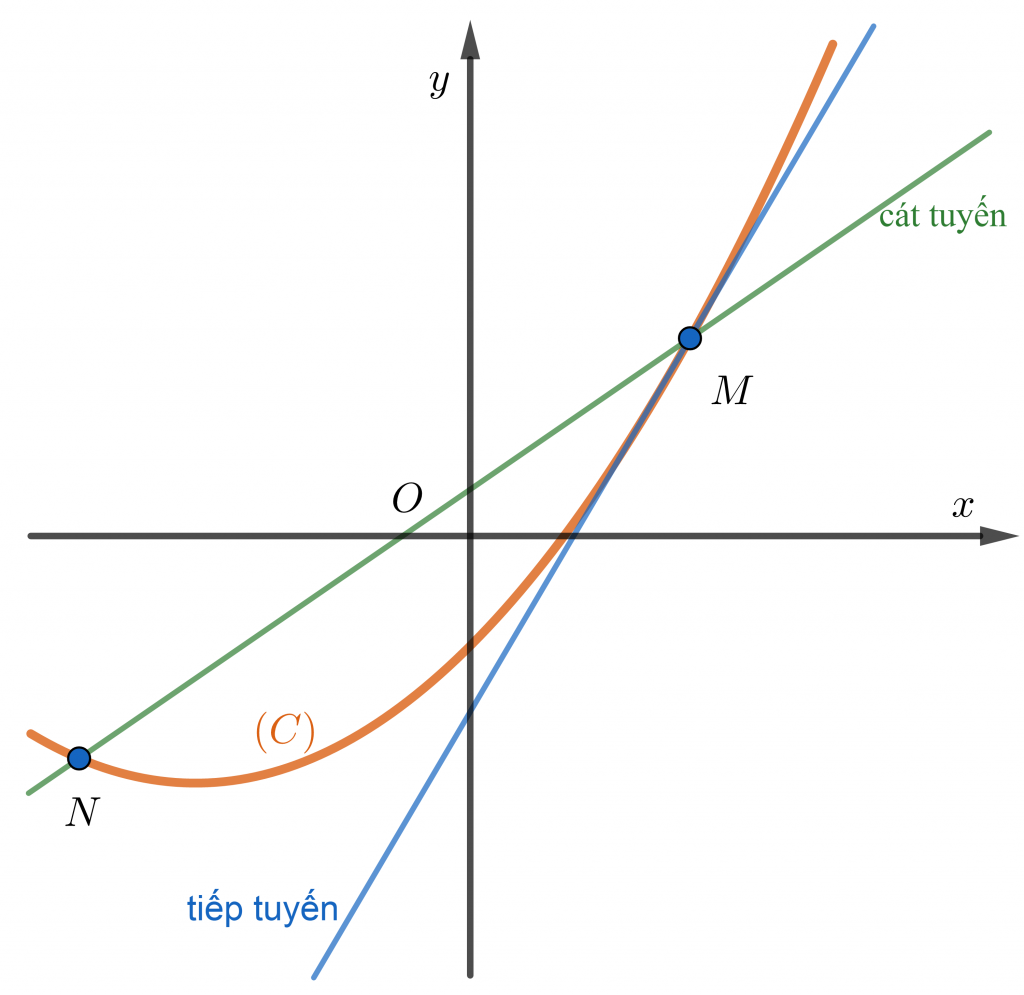
tiếp tuyến của đồ thị hàm số

Tiếp tuyến của đồ thị hàm số

Nếu hàm y=f(x) có đạo hàm tại điểm α thì phương trình tiếp tuyến tại α là: y=y'(α)(x-α)+y(α).

VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ

VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN KHI BIẾT ĐIỂM NẰM TRÊN ĐỒ THỊ

Bài toán: Cho hàm số y=f(x) có đồ thị (C) và điểm M(α;f(α)) nằm trên (C). Hàm y=f(x) có đạo hàm tại điểm α. Yêu cầu viết phương trình tiếp tuyến tại điểm M.

Phương pháp: Ở dạng này chúng ta chỉ cần tính thêm giá trị y'(α) và thay vào công thức y=y'(α)(x-α)+y(α).

Lưu ý: Đề bài thường không nói điểm đó có nằm trên đồ thị hay không. Nên trước tiên chúng ta cần kiểm tra điểm có nằm trên đồ thị hay không đã.

Ví dụ:

Viết phương trình tiếp tuyến của đồ thị hàm y=x²+x đi qua điểm M(1;2).

Lời giải:

Kiểm tra thấy điểm M nằm trên đồ thị hàm số đã cho.

Ta có: y’=2x+1⇒y'(1)=3.

Vậy phương trình tiếp tuyến cần tìm là: y=3(x−1)+2⇔y=3x−1.

VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN KHI BIẾT HOÀNH ĐỘ TIẾP ĐIỂM

Bài toán: Cho hàm số y=f(x) có đạo hàm tại điểm α và yêu cầu viết phương trình tiếp tuyến tại α .

Phương pháp: Trường hợp này khác trường hợp bên trên 1 chút. Đó là chúng ta không cần kiểm tra điểm nằm trên đồ thị. Nhưng chúng ta cần tính thêm giá trị y(α) và tất nhiên vẫn phải tính giá trị y'(α) rồi.

Ví dụ:

Viết phương trình tiếp tuyến của đồ thị hàm y=x³−3x tại điểm x=2.

Lời giải:

Ta có: y’=3x²-3.

y'(2)=9 và y(2)=2.

Vậy phương trình tiếp tuyến cần tìm là: y=9(x−2)+2⇔y=9x−16.

Bộ đề thi Online các dạng có giải chi tiết: Phương trình tiếp tuyến

VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN KHI BIẾT TUNG ĐỘ TIẾP ĐIỂM

Bài toán: Cho hàm số y=f(x). Yêu cầu viết phương trình tiếp tuyến biết tung độ tiếp điểm β.

Phương pháp: Với dạng toán này chúng ta cần giải phương trình y(x)=β để tìm tung độ tiếp điểm. Từ hoành độ tiếp điểm chúng ta tìm được hệ số góc bằng cách thay vào y’.

Ví dụ:

Viết phương trình tiếp tuyến của đồ thị hàm y=x²−1 biết tung độ tiếp điểm là 8.

Lời giải:

y’=2x.

Ta có: x²−1=8⇔ x²=9⇔x=±3.

Với x=3 thì y'(3)=6. Do đó phương trình tiếp tuyến cần tìm là y=6(x−3)+8⇔y=6x−10.

Với x=−3 thì y'(−3)=−6. Do đó phương trình tiếp tuyến cần tìm là y=−6(x+3)+8⇔y=−6x−10.

Vậy có 2 phương trình tiếp tuyến thỏa mãn yêu cầu bài toán là y=6x−10 và y=−6x−10.

VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN KHI BIẾT HỆ SỐ GÓC

Bài toán: Cho hàm số y=f(x). Yêu cầu viết phương trình tiếp tuyến có hệ số góc k.

Phương pháp: Dạng toán này còn thường xuất hiện dưới dạng viết phương trình tiếp tuyến song song hoặc vuông góc với đường thẳng cho trước. Để là dạng toán này ta giải phương trình y'(x)=k để tìm tung độ tiếp điểm.

Ví dụ:

Viết phương trình tiếp tuyến của đồ thị hàm y=−x²+3x+1 song song với đường thẳng y=x.

Lời giải:

Ta có: y’=−2x+3.

Vì tiếp tuyến song song với đường thẳng y=x nên y’=1⇔−2x+3=1⇔x=1.

Ta lại có: y(1)=3.

Vậy phương trình tiếp tuyến cần tìm là: y=1(x−1)+3⇔y=x+2.

VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN ĐI QUA ĐIỂM NẰM NGOÀI ĐỒ THỊ HÀM SỐ

Bài toán: Cho hàm số y=f(x) có đồ thị (C). Điểm M(α;β) nằm ngoài đồ thị (C). Yêu cầu viết phương trình tiếp tuyến của (C) đi qua M.

Phương pháp: Có thể thấy dạng này “khó” hơn các dạng trên. Để giải dạng toán này chúng ta sử dụng điều kiện tiếp xúc của hai đường cong.

Điều kiện tiếp xúc trong viết phương trình tiếp tuyến của đồ thị hàm số

Ví dụ: 

Cho hàm số y=x²+2x−4 (C). Viết phương trình tiếp tuyến của (C) đi qua điểm M(2;0).

Lời giải:

Kiểm tra thấy điểm M không nằm trên (C).

Phương trinh đường thẳng d đi qua M có dạng y=k(x−2).

Để d là tiếp tuyến của (C) thì hệ sau phải có nghiệm và nghiệm chính là hoành độ tiếp điểm.

Với k=2, phương trình tiếp tuyến là y=2x−4.

Với k=10, phương trình tiếp tuyến là y=10x−20.

Nhận xét chung: Các dạng toán trên đều quy về tìm hoành độ tiếp điểm.

Chúc các em thành công!

Bộ đề thi Online các dạng có giải chi tiết: Phương trình tiếp tuyến

Hàm số -