Hàm số bậc nhất – Dạng bài tập thường gặp
Hàm số bậc nhất có những dạng bài tập nào thường gặp. Cách giải quyết các bài toán đó như thế nào ? Bài viết dưới đây sẽ hướng dẫn các em.
Content
HÀM SỐ BẬC NHẤT
Hàm bậc nhất có dạng y=ax+b (a≠0) trong đó a và b là các hằng số.
✔ Tập xác định : R.
✔ Sự biến thiên: Nếu a>0 thì hàm số đồng biến trên R. Ngược lại, nếu a<0 thì hàm số nghịch biến trên R.
✔Đồ thị: Đồ thị hàm số y=ax+b là một đường thẳng.
DẠNG TOÁN HÀM SỐ BẬC NHẤT LỚP 9
Dạng 1: Vẽ đồ thị hàm số
Dạng toán này có từ lớp 7 đến lớp 10 và tập trung ở lớp 9,10. Để vẽ đồ thị hàm số y=ax+b ta xác định hai điểm bất kỳ phân biệt nằm trên đường thẳng. Sau đó vẽ đường thẳng đi qua hai điểm đó là được.
Ví dụ:
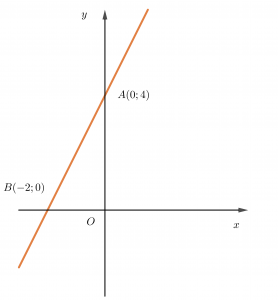
Vẽ đồ thị hàm số y=2x+4.
Lời giải:
Đường thẳng y=2x+4 đi qua các điểm A(0;4) và B(-2;0). Từ đó ta vẽ được đồ thị hàm số.
Dạng 2: Xác định đường thẳng song song hay vuông góc với đường thẳng cho trước
Điều kiện để hai đường thẳng y=ax+b và y=αx+β song song với nhau là a=α và b≠β.
Còn điều kiện để hai đường thẳng y=ax+b và y=αx+β vuông góc với nhau là aα=−1.
Khi gặp dạng toán này ta cứ áp dụng 2 điều kiện trên là được.
Ví dụ 1:
Xác định đường thẳng đi qua A(1;3) song song với đường thẳng y=−2x+6.
Lời giải:
Đường thẳng song song với đường thẳng y=−2x+6 có phương trình dạng y=−2x+m (lưu ý hai đường thẳng song song phần hệ số góc bằng nhau) với m≠6.
Thay x=1, y=3 vào phương trình ta được 3=−2.1+m⇔m=5.
Vậy phương trình đường thẳng cần tìm là y=−2x+5.
Ví dụ 2:
Tìm đường thẳng đi qua A(3;2) và vuông góc với đường thẳng y=x+1.
Lời giải:
Giả sử đường thẳng y=ax+b vuông góc với đường thẳng đã cho.
Suy ra 1.a=−1⇔a=−1.
Thay x=3, y=2, a=−1 vào phương trình ta có: 2=−3+b⇔b=5.
Vậy phương trình đường thẳng cần tìm là y=−x+5.
DẠNG TOÁN HÀM SỐ BẬC NHẤT LỚP 10
Dạng 3: Tìm tham số để hàm số đồng biến, nghịch biến
Thực ra dạng toán này có từ lớp 9 nhưng rõ ràng hơn ở lớp 10. Để làm dạng toán này chúng ta chỉ cần đánh giá hệ số của x là đủ.
Ví dụ 1:
Tìm m để hàm số y=(m-2)x+3 đồng biến trên R.
Lời giải:
Để hàm số đã cho đồng biến trên R thì m−2>0⇔m>2.
Ví dụ 2:
Tìm số giá trị nguyên của tham số m để hàm số y=(m²−4)x+m−3 nghịch biến trên R.
Lời giải:
Để hàm số đã cho nghịch biến trên R thì m²−4<0⇔−2<m<2.
Vậy có đúng 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chúc các em thành công!
Xem thêm:
Hàm số bậc nhất bậc 2 -