Tìm giá trị min max số phức z như thế nào?
Min max số phức là một dạng toán vận dụng, vận dụng cao về số phức. Lời giải các bài toán dạng này thường đa dạng nên không có 1 phương pháp chung giải cho tất cả các bài toán. Tuy nhiên chúng ta có thể phân ra 2 loại phương pháp chính là phương pháp hình học và phương pháp đại số. Còn để chi tiết hơn, bài viết dưới đây tôi sẽ nêu ra 1 số dạng max mιn số phức mà ta hay gặp. Các bạn cùng theo dõi nhé!
Content
I. TÌM MIN MAX SỐ PHỨC Z CÓ QUỸ TÍCH ĐIỂM BIỂU DIỄN LÀ ĐƯỜNG THẲNG
Trên mặt phẳng phức thì phương trình đường thẳng có thể được biểu diễn dưới dạng
|z-(a+bi)|=|z-(c+di)|. (*)
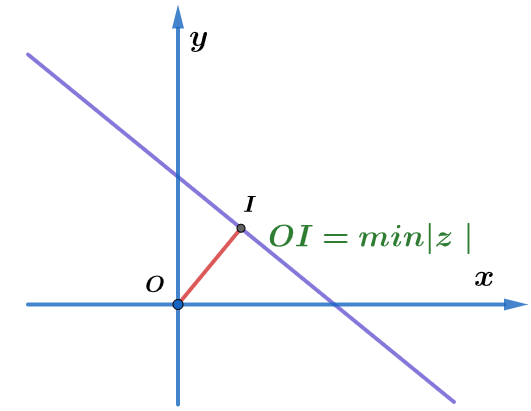
Thực vậy, giả sử điểm M biểu diễn cho số phức a+bi. Điểm N biểu diễn cho số phức c+di. Điểm A biểu diễn cho số phức z. Thì |z-(a+bi)| biểu diễn bởi độ dài đoạn AM. Còn |z-(c+di)| biểu diễn bởi độ dài đoạn AN. Do đó phương trình (*) được biểu diễn bởi các điểm cách đều M và N. Hay nói cách khác (*) là phương trình trung trực đoạn MN.
Ngược lại, mỗi đường thẳng trong mặt phẳng phức đều có thể chọn lấy 2 điểm M, N. Sao cho đoạn MN nhận đường thẳng đó là đường thẳng trung trực. Tức là ta có thể quy về phương trình dạng (*).
Vấn đề tiếp theo là trong các số phức z thảo mãn (*) ta tìm số phức có modun nhỏ nhất.
Thật đơn giản, theo những phân tích ở trên ta chỉ việc tìm hình chiếu của O (gốc tọa độ) lên đường thẳng. Còn nếu bài toán yêu cầu ta tính giá trị nhỏ nhất của |z| thì ta chỉ cần tính khoảng cách từ O đến đường thẳng.
Ví dụ minh họa:
Cho số phức z thỏa mãn phương trình |z-(1+2i)|=|z-(3+i)|. Tìm số phức z có mô đun nhỏ nhất.
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
II. TÌM MIΝ MAX SỐ PHỨC Z CÓ QUỸ TÍCH ĐIỂM BIỂU DIỄN LÀ ĐƯỜNG TRÒN
Như ta đã biết trên mặt phẳng phức thì phương trình đường tròn có dạng
|z-(a+bi)|=r (**)
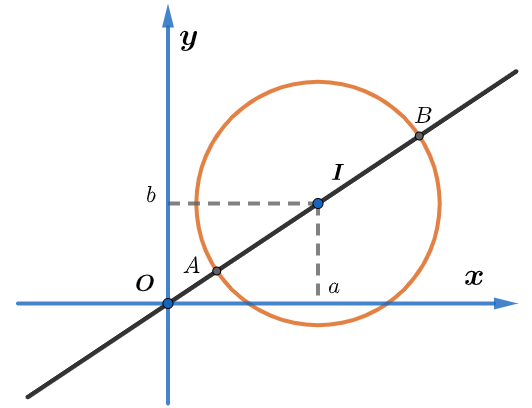
Thực vậy giả sử điểm I biểu diễn cho số phức a+bi. Điểm M biểu diễn cho số phức z. Thì |z-(a+bi)| được biểu diễn bởi độ dài đoạn MI. Vậy điểm M luôn cách điểm I một khoảng không đổi bằng r. Hay nói cách khác (**) chính là phương trình đường tròn tâm I(a;b) và bán kính r. Ngược lại, mọi đường tròn trên mặt phẳng phức đều có thể biểu diễn bởi phương trình dạng (**).
Gọi A và B là 2 giao điểm của đường thẳng OI và đường tròn (**).
Dựa vào các phân tích trên ta suy ngay ra được 1 trong 2 điểm A, B sẽ biểu diễn cho số phức có mô đun nhỏ nhất. Điểm còn lại sẽ biểu diễn cho số phức có mô đun lớn nhất. Còn nếu bài toán chỉ yêu cầu tìm mô đun lớn nhất hay nhỏ nhất của z thì ta lấy OI+r hoặc OI-r.
Ví dụ minh họa:
Cho số phức z thỏa mãn |z-(4+3i)|=5. Tìm giá trị lớn nhất của |z|.
Lời giải:
Tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(4;3) bán kính r=5. Vậy giá trị lớn nhất của |z| là
III. TÌM MAX MIN SỐ PHỨC Z CÓ QUỸ TÍCH ĐIỂM BIỂU DIỄN LÀ ĐƯỜNG ELIP
Trong mặt phẳng phức, phương trình chính tắc của Elip có dạng
|z-c|+|z+c|=2a (a>c>0). (***)
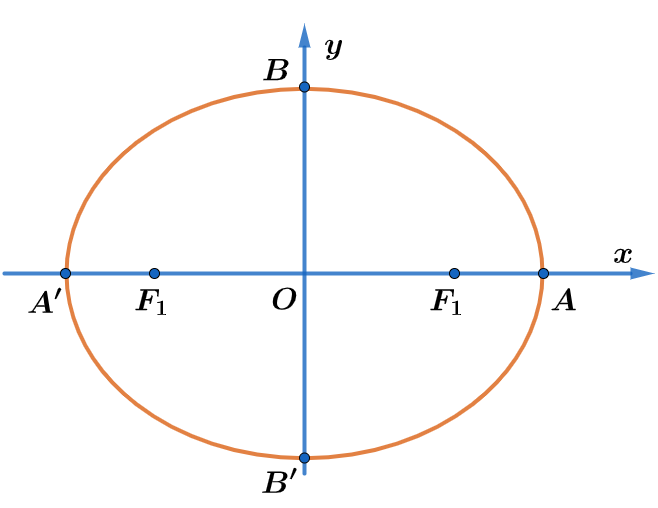
Như ta đã biết Elip là quỹ tích các điểm có tổng khoảng cách đến 2 điểm (tiêu điểm) cho trước không đổi. Do đó phương trình (***) chính là phương trình 1 Elip. Hai tiêu điểm (-c;0) và (c;0) nằm trên trục hoành nên (***) là phương trình chính tắc.
Ta có thể thấy trong trường hợp này, mô đun nhỏ nhất của số phức z bằng b (b là nửa độ dài trục nhỏ) khi z=±bi. Mô đun lớn nhất của số phức z bằng a ( nửa độ dài trục lớn) khi z=±a.
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
Ví dụ minh họa:
Cho số phức z thỏa mãn |z-3|+|z+3|=10. Biết giá trị lớn nhất của |z| là M, giá trị nhỏ nhất của |z| là m. Tính M+m.
Lời giải:
Ta thấy quỹ tích điểm biểu diễn số phức z là Elip có độ dài trục lớn là 2a=10, tiêu cự là 2c=6, độ dài trục nhỏ là 2b=8 (do a²=b²+c²). Từ đó suy ra M=5 và m=4.
Vậy M+m=9.
Năm nay Bộ GD tinh giản nội dung max min số phức nên tôi xin phép tạm dừng bài viết tại đây. Chúc các bạn thành công!
Xem thêm:
Khái niệm tổng quan về số phức
Giải phương trình số phức như thế nào?
Tìm số phức z có môđun nhỏ nhất hoặc lớn nhất
Số Phức -Tìm số phức z có môđun nhỏ nhất hoặc lớn nhất
Modun số phức và các tính chất liên quan
Cách bấm máy tính số phức trên CASIO 580 VNX
Dạng lượng giác của số phức và ứng dụng
Phép chia số phức thực hiện như thế nào ?
Tìm số phức z thỏa mãn điều kiện cho trước
Tìm tập hợp điểm biểu diễn số phức như thế nào ?