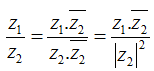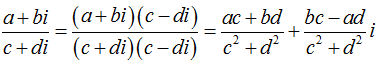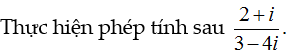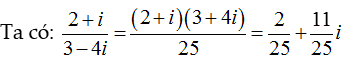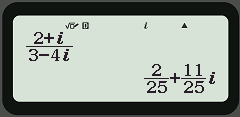Phép chia số phức thực hiện như thế nào ?
Phép chia số phức là một trong các phép toán của số phức. Vậy cụ thể phép toán chia sô’ phức được thực hiện như thế nào. Các em cùng theo dõi bài viết dưới đây để tìm hiểu nhé!
Content
SỐ PHỨC LIÊN HỢP
Trước hết chúng ta cùng nhắc lại khái niệm số phức liên hợp.
Như vậy chúng ta có thể thấy hai số phức liên hợp thì phần thực bằng nhau và phần ảo thì đối nhau. Do đó về mặt biểu diễn hình học thì điểm biểu diễn của hai số phức liên hợp đối xứng nhau qua trục thực.
Tính chất: Trong nội dung bài này chúng ta chỉ quan tâm tới 1 tính chất sau:
Theo tính chất ta thấy nếu lấy tích của số phức và số phức liên hợp của nó ta được 1 số thực. Từ đó ta vận dụng tính chất trên vào để thực hiện phép chia 2 số phức.
PHÉP CHIA SỐ PHỨC
Để thực hiện phép chia hai sô’ phức ta thực hiện nhân cả tử (Số bị chia) và mẫu (Số chia) với số phức liên hợp của mẫu (Số chia).
Hoặc cụ thể hơn:
Tuy nhiên, thực tế tính toán chúng ta nên nhớ nguyên tắc tính chứ không nên nhớ công thức.
Ví dụ minh họa:
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
THỰC HIỆN CÁC PHÉP TOÁN SỐ PHỨC TRÊN MÁY TÍNH CASIO 580VNX
Trong các máy tính bỏ túi đều có môi trường số phức. Đối với máy tính Casio 580VNX ta bấm MODE 2 để thiết lập môi trường số phức.
Các chức năng đều tập trung ở phím OPTN. Trong chương trình trung học phổ thông hiện nay chúng ta chỉ quan tâm đến 1 số chức năng sau:
- Conjugate: Cho ra kết quả là số phức liên hợp.
- Real Part: Cho ra kết quả là phần thực của số phức.
- Imaginary Part: Cho ra kết quả là phần ảo của số phức.
- Argument: Cho ra kết quả là argument của số phức.
Còn để thực hiện các phép toán số phức thì ta nhập phép tính vào và bấm dấu = là được kết quả. Chẳng hạn ta xét lại ví dụ bên trên:
Ví dụ:
Các bước thực hiện:
MODE2 sau đó nhập các phép tính. Để bấm đơn vị ảo ta bấm ENG.
Sau đó ấn dấu = là được kết quả. Các phép toán cộng trừ nhân đều thực hiện được.
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
Chúc các em thành công!
Xem thêm:
Số Phức -