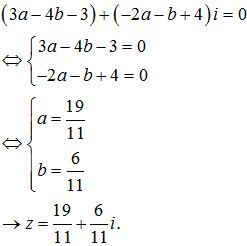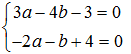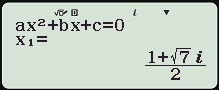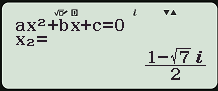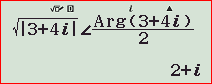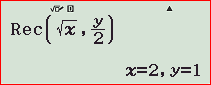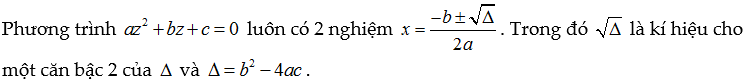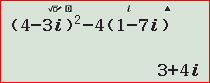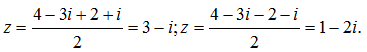Cách bấm máy tính số phức trên CASIO 580 VNX
Cách bấm máy tính số phức trên máy tính bỏ túi CASIO 580 VNX như thế nào? Nếu quá mệt mỏi với việc biến đổi phương trình số phức thì các bạn có thể đọc bài viết sau. Toanthaydinh.com sẽ chỉ cho các bạn cách nhanh nhất để giải một phương trình số phức với trợ thủ đắc lực là máy tính bỏ túi. Ở bài viết này chúng ta sẽ thực hành trên máy tính bỏ túi CASIO 580 VNX. Chúng ta hoàn toàn có thể thực hành tương tự trên các dòng máy khác nếu chúng ta đọc bài viết này và nắm được các nguyên tắc. Cùng bắt đầu nhé!
Content
- 1 I. MÔI TRƯỜNG SỐ PHỨC VÀ TÍNH NĂNG VỀ SỐ PHỨC TRÊN MÁY CASIO 580VNX
- 2 II. CÁCH GIẢI PHƯƠNG TRÌNH SỐ PHỨC BẰNG MÁY TÍNH
I. MÔI TRƯỜNG SỐ PHỨC VÀ TÍNH NĂNG VỀ SỐ PHỨC TRÊN MÁY CASIO 580VNX
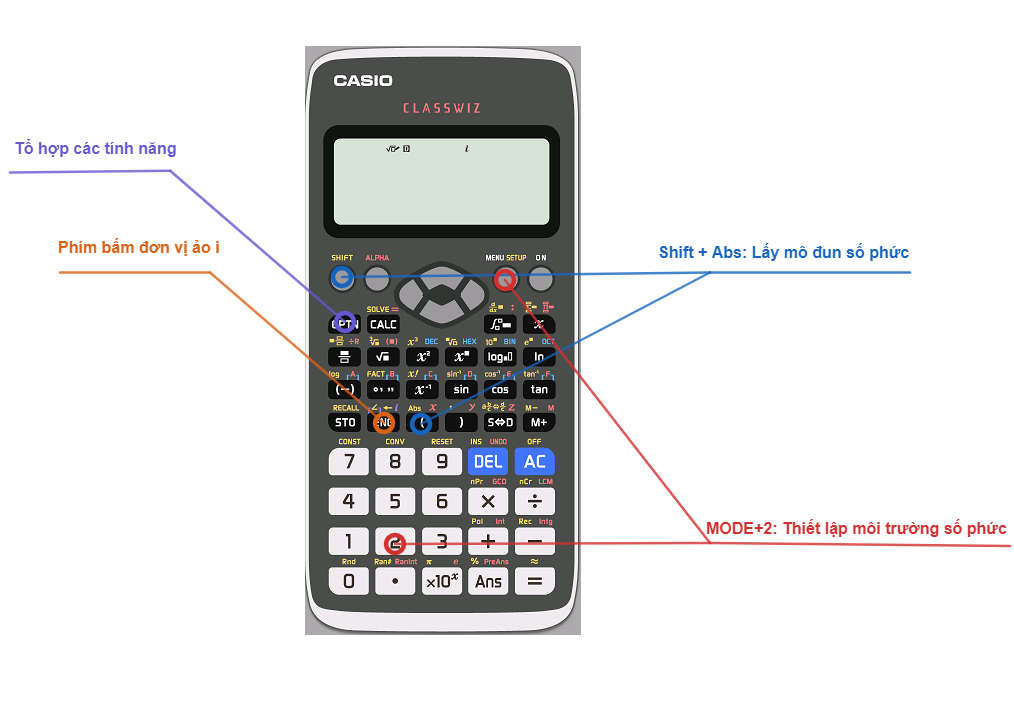
1. CÁCH BẤM MÁY TÍNH SỐ PHỨC CÁC PHÍM BẤM CƠ BẢN
Thiết lập môi trường tính toán số phức với lệnh MODE 2. Làm gì thì làm nhưng muốn làm việc với số phức thì ta phải thiết lập môi trường số phức đã. Khi bấm MODE 2 xong các bạn sẽ thấy góc bên trên màn hình có chữ i. Có nghĩa là môi trường số phức đã được thiết lập.
Tiếp theo, chúng ta cần chú ý tổ hợp phím Shift+Abs. Ngoài môi trường số phức thì tổ hợp phím này sẽ cho chúng ta giá trị tuyệt đối của một số. Còn trong môi trường số phức thì nó sẽ cho chúng ta giá trị mô đun của một số phức. Ví dụ như khi ta bấm Shift Abs 3+4i= ta sẽ được kết quả là 5.
À, vậy còn đơn vị ảo i chúng ta bấm như thế nào? Ta bấm ENG nhé. Chứ đừng bấm Shift+ENG. Vì Shift+ENG là bấm góc ở dạng lượng giác của số phức. Chúng ta sẽ bàn ở phần sau của bài viết này nhé.
Cuối cùng là phím bấm quyền lực nhất OPTN. Từ các phiên bản máy tính 580, Casio đã gom các tính năng trong tất cả các môi trường tính toán vào một phím duy nhất là phím OPTN ở góc bên trái dưới phím Shift quen thuộc. Chúng ta hãy cùng khám phá các tính năng đứng đằng sau phím này trong môi trường số phức qua hình ảnh dưới đây.
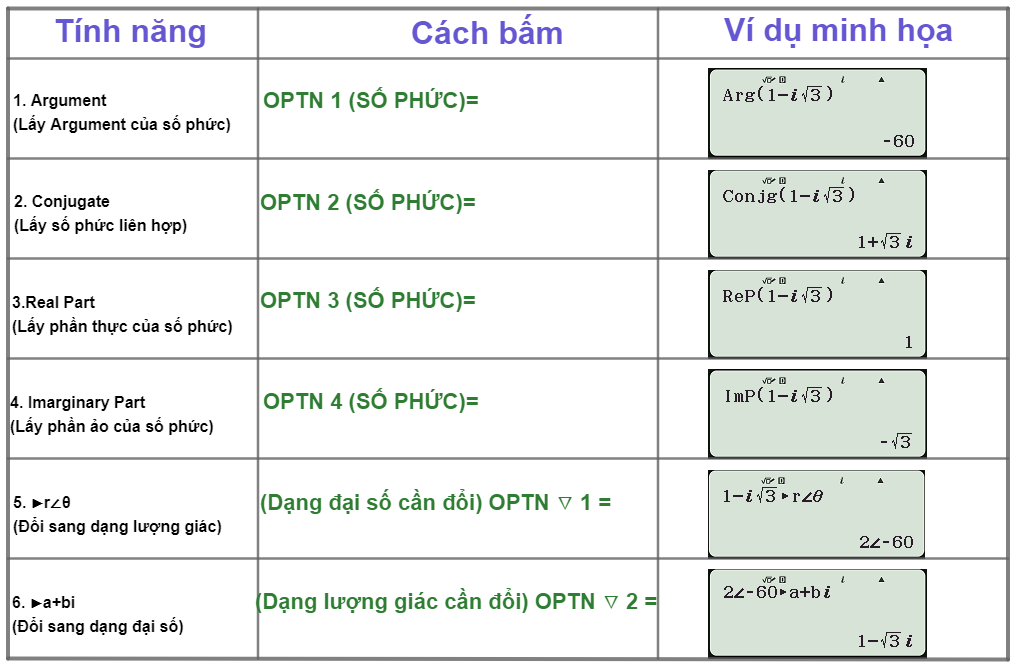
2. CÁCH BẤM MÁY TÍNH SỐ PHỨC CÁC TÍNH NĂNG TRONG PHÍM OPTN
Trong môi trường số phức khi ta bấm vào “phím quyền lực” OPTN thì hàng loạt các tính năng hiện ra cho chúng ta lựa chọn. Tuy nhiên chúng ta phải hiểu rõ từng tính năng thì mới sử dụng được. Đứng ở vị trí đầu tiên là tính năng lấy Argument của 1 số phức. Sau khi bấm OPTN và phím 1, ta chỉ cần nhập số phức cần bấm Argument vào (không cần đóng ngoặc cũng được) và bấm dấu = là chúng ta đã có kết quả. Các tính năng tiếp theo lần lượt là: Lấy số phức liên hợp; Tìm phần thực phần ảo của số phức bằng máy tính; Đổi sạng dạng lượng giác của số phức và ngược lại (2 chức năng này sau khi bấm OPTN phải bấm nút kéo xuống mới thấy.
Một trong các vấn đề chúng ta cũng rất quan tâm đó là giải phương trình số phức bằng máy tính. Đây là phần quan trọng nhất của bài viết này. Hãy theo dõi phần tiếp theo của bài viết để tìm hiểu nhé.
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
II. CÁCH GIẢI PHƯƠNG TRÌNH SỐ PHỨC BẰNG MÁY TÍNH
Trong môi trường số phức chúng ta không sử dụng được chức năng Shift+Solve để tìm nghiệm gần đúng. Vì vậy chúng ta sử dụng chức năng CALC. Trước hết để tiện việc tính toán ta chia thành các trường hợp sau để giải quyết: Phương trình bậc nhất; Phương trình bậc 2, bậc 3, bậc 4 với hệ số thực; Phương trình có chứa ít nhất 2 đại lượng trong 3 đại lượng z, liên hợp của z, mô đun của z.
1. CÁCH BẤM MÁY TÍNH SỐ PHỨC GIẢI PHƯƠNG TRÌNH BẬC NHẤT
Đối với phương trình bậc nhất đối với số phức z (hoặc đối với số phức liên hợp của z) ta rút z (hoặc đối với số phức liên hợp của z) ra sau đó bấm máy để thực hiện phép tính.
Ví dụ minh họa:
Tìm số phức z thỏa mãn: (2+3i)z-3+2i=4i-5.
Lời giải:
Đối với phương trình bậc nhất ta chỉ nên làm như vậy. Chúng ta không cần dùng thêm thủ thuật gì vì như vậy là nhanh nhất rồi. Còn nếu bạn đủ bản lĩnh thì không ai cấm bạn giải phương trình trên theo cách dưới đây cả.
2. CÁCH BẤM MÁY TÍΝH SỐ PHỨC GIẢI PHƯƠNG TRÌNH CÓ CẢ Z VÀ SỐ PHỨC LIÊN HỢP CỦA Z
Trước tiên chúng ta cần nắm được cái nguyên tắc của cách bấm dạng toán này đã. Toanthaydinh.com cũng đã tham khảo rất rất nhiều bài viết cũng như Video về vấn đề này. Nhưng chưa thấy ai giải thích. Mà chỉ có hướng dẫn bấm choách choách choách. Rất nguy hiểm khi bấm máy tính mà chúng ta không hiểu bản chất của bài toán.
Trước tiên hãy cùng xét một ví dụ và giải nó theo cách thông thường:
Ví dụ minh họa:
Tìm số phức z thỏa mãn phương trình sau:
Lời giải:
Giả sử z=a+bi (a,b∈R) thì qua vài bước biến đổi ta được:
Bây giờ ta hãy lưu ý ở bước hệ phương trình
Nếu ta có thể “mò” ra được hệ này. Chúng ta có thể lược bỏ bớt ở bước biến đổi phương trình. Nếu chúng ta thay a=1000, b=0,01 thì rõ ràng ở phương trình đầu 3a là 1 số rất lớn(=3000) còn -4b là 1 số rất nhỏ (=-0,04). Hoàn toàn như vậy ở phương trình thứ 2. Tóm lại, thay a bằng 1 số lớn, b bằng 1 số nhỏ chúng ta có thể phân tích để “mò” được hệ phương trình. Còn việc thay và giải hệ thì máy tính bỏ túi lại thực hiện được rất nhanh.
* BẤM MÁY TÍNH GIẢI PHƯƠNG TRÌNH SỐ PHỨC
Cụ thể chúng ta có thể bấm máy giải phương trình trên như sau:
Trong môi trường số phức (MODE 2) bấm: (1+i)x+(2-3i)conjg(x)-3+4i. Tiếp theo bấm CALC 1000+0.01i và bấm =.
Bấm phím S⇔D để đưa về dạng số thập phân.
Đến đây ta phân tích phần thực của kết quả vừa thu được theo 2 số 1000 và 0.01. Ta được:
2996,96=3.1000-4.0,01-3 và -1996,01=-2.1000-0,01+4.
Từ đó ta thu được hệ
Vào chức năng MODE 9 để giải hệ phương trình bậc nhất 2 ẩn ta thu được kết quả.
Vậy sự thực trong quá trình bấm máy tính đã có yếu tố mò mẫm. Hơn nữa nếu phương trình chứa mô đun nữa thì phân tích phức tạp hơn vì có chứa ẩn bậc 2. Nên nếu chúng ta quyết định sử dụng cách này chúng ta cần luyện tập nhiều để rút kinh nghiệm. Còn toanthaydinh.com vẫn khuyên các bạn chịu khó biến đổi theo cách giải thông thường và dùng máy tính bấm hỗ trợ các phép tính số phức thôi nhé.
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
3. CÁCH BẤM MÁY TÍΝH SỐ PHỨC GIẢI PHƯƠNG TRÌNH BẬC 2, BẬC 3, BẬC 4 VỚI HỆ SỐ THỰC
Đối với phương trình bậc 2, bậc 3, bậc 4 với hệ số thực chúng ta không giải trong môi trường số phức MODE 2. Mà ta giải bằng chức năng MODE 9 2 (bậc của phương trình).
Kết quả thu được sẽ bao gồm cả các nghiệm thực và các nghiệm phức (nếu có) của phương trình.
Chẳng hạn bấm máy tính giải phương trình: x²-x+2=0 ta được kết quả như hình dưới đây.
- Nhập hệ số
- Bấm =
- Bấm =
Từ đó ta thu được 2 nghiệm phức của phương trình đã cho.
4. CÁCH BẤM MÁY TÍΝH SỐ PHỨC GIẢI PHƯƠNG TRÌNH BẬC 2 VỚI HỆ SỐ PHỨC
Lưu ý đây là 1 nội dung được giảm tải nên các bạn có thể bỏ qua nếu thấy không cần thiết.
4.1. CÁCH BẤM CĂN BẬC 2 CỦA MỘT SỐ PHỨC
Mỗi số phức z đều có 2 căn bậc 2 là w và -w. Trong đó w thỏa mãn w²=z.
Có 2 cách để chúng ta bấm căn bậc 2 của 1 số phức. Ví dụ chúng ta cần bấm căn bậc 2 của số phức 3+4i.
Cách 1: Trong môi trường số phức (MODE 2) ta bấm như hình dưới. Giải thích: Phần bên trái là căn mô đun của 3+4i, phần bên phải là 1 nửa Argument của 3+4i.
Như vậy số phức 3+4i có 2 căn bậc 2 là 2+i và -2-i.
Cách 2: Trong môi trường Calculate (MODE 1) ta bấm như hình dưới.
Giải thích: Bước đầu (Hình thứ nhất) ta chuyển điểm (3;4) về tọa độ cực. Bước tiếp theo (Hình thứ 2) ta tính 1 căn bậc 2 của số phức 3+4i. Vậy số phức 3+4i có 2 căn bậc 2 là 2+i và -2-i.
4.2. CÁCH BẤM GIẢI PHƯƠNG TRÌNH BẬC 2 VỚI HỆ SỐ PHỨC
Nói chung phương trình bậc 2 với hệ số phức cũng được giải tương tự như phương trình bậc 2 với hệ số thực. Tức là tính Delta và áp dụng công thức nghiệm.
Ví dụ minh họa:
Giải phương trình sau z²-(4-3i)z+1-7i=0.
Cách bấm máy tính bỏ túi:
Trước tiên vào môi trường số phức MODE 2 bấm Delta như hình
Ồ, thật ngẫu nhiên toanthaydinh.com lại chọn được 1 ví dụ có Delta giống với ví dụ bên trên. Các bạn kéo lên trên để xem lại cách bấm căn bậc 2 của Delta nhé.Vậy phương trình đã cho có 2 nghiệm là
Như vậy toanthaydinh.com đã hướng dẫn các bạn gần như hết các cách bấm máy tính trên tập số phức rồi đó. Việc tiếp theo của các bạn là dựa vào đó để luyện tập luyện tập và luyện tập sao cho thật nhuần nhuyễn.
Chúc các bạn thành công!
Xem thêm:
Số Phức -