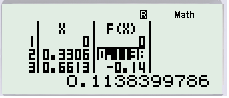Giá trị lớn nhất nhỏ nhất của hàm số
Giá trị lớn nhất giá trị nhỏ nhất của hàm số (gtln, gtnn) là gì? Bài viết sau đây sẽ đưa ra định nghĩa về gtln, gtnn của hàm số và những lưu ý trước khi làm dạng toán này.
Content
ĐỊNH NGHĨA GTLN, GTNN CỦA HÀM SỐ
Như vậy chúng ta cần hiểu rằng gtln, gtnn của hàm số trên đoạn (khoảng) là phải đạt được tại ít nhất một điểm trên đoạn (khoảng) đó. Tức là có những hàm số không có gtln hay gtnn mặc dù nó có cận trên và cận dưới trên đoạn (khoảng) đang xét.
Ví dụ:
Mặc dù giá trị hàm số y=1/x luôn dương trên (0;+∞) nhưng nó lại không có giá trị nhỏ nhất trên (0;+∞). Hàm số nêu trên chỉ có giá trị cận dưới là 0 trên (0;+∞) mà thôi.
PHÂN CHIA BÀI TẬP GIÁ TRỊ LỚN NHẤT GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Bài tập gtln, gtnn xuất hiện trong chương trình cả ba khối THPT. Ở lớp 10 bài tập gtln, gtnn có trong phần hàm số bậc 2. Lớp 11 thì xuất hiện ở phần gtln, gtnn của hàm số lượng giác. Giá trị lớn nhất nhỏ nhất của hàm số lop 12 thì nhiều ở trong chương 1: “Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số”. Tất nhiên cách giải của lớp 12 là dùng đạo hàm sẽ áp dụng được cho cả lớp 10 và lớp 11. Chúng ta tạm phân chia như vậy để “hình dung” ra được lượng kiến thức của dạng bài tập tìm gtln, gtnn của hàm số.
Ví dụ:
Chúng ta lấy ví dụ về 3 dạng bài tập kể trên. Tuy nhiên chúng ta chưa đề cập đến vấn đề giải bài tập đó như thế nào trong bài viết này. Cách giải các dạng toán này theo từng khối lớp sẽ được đề cập đến trong các bài viết sau dưới phần xem thêm.
Bài 1: (Lớp 10) Tìm gtln của hàm số y=−2x²+3x+2.
Bài 2: (Lớp 11) Tìm gtln, gtnn của hàm số y=2sin(2x+2)-3.
Bài 3: (Lớp 12) Tìm gtln,gtnn của hàm số y=lnx+2x-3 trên [1;5].
Bộ đề thi Online các dạng có giải chi tiết: GTLN-GTNN của Hàm số
Tìm giá trị lớn nhất nhỏ nhất của hàm số lớp 12
Tìm giá trị lớn nhất nhỏ nhất của hàm số lớp 12 như thế nào? Ở lớp 12 chúng ta chủ yếu tìm gtln, gtnn của hàm số bằng cách sử dụng đạo hàm. Trong một số trường hợp ta kết hợp sử dụng thêm bất đẳng thức và máy tính bỏ túi để tăng tốc độ giải quyết bài toán trắc nghiệm.
ĐỊNH NGHĨA GTLN, GTNN CỦA HÀM SỐ
Như vậy chúng ta cần hiểu rằng gtln, gtnn của hàm số trên đoạn (khoảng) là phải đạt được tại ít nhất một điểm trên đoạn (khoảng) đó. Tức là có những hàm số không có gtln hay gtnn mặc dù nó có cận trên và cận dưới trên đoạn (khoảng) đang xét.
Ví dụ:
Mặc dù giá trị hàm số y=1/x luôn dương trên (0;+∞) nhưng nó lại không có giá trị nhỏ nhất trên (0;+∞). Hàm số nêu trên chỉ có giá trị cận dưới là 0 trên (0;+∞) mà thôi.
CÁCH TÌM GTLN, GTNN CỦA HÀM SỐ BẰNG ĐẠO HÀM
tTìm gtln, gtnn của hàm số trên đoạn với tìm gtln gtnn của hàm số trên khoảng hoàn toàn tương tự nhau. Để tìm GTLN, GTNN của hàm số trên khoảng (a;b) hay đoạn [a;b] ta thực hiện theo các bước sau:
Bước 1: Tìm các nghiệm của đạo hàm hoặc những điểm tại đó đạo hàm không xác định.
Bước 2: Lập bảng biến thiên. ( Trên đoạn có thể không cần lập bảng biến thiên). Lưu ý điểm nay
Bước 3: Từ bảng biến thiên so sánh các giá trị của hàm số và đưa ra kết luận.
Ví dụ:
Tìm GTLN, GTNN của hàm số trên [-3;4].
Lời giải:
Chú ý: Với các hàm số mà chưa chỉ rõ xét trên tập nào thì ta cần tìm tập xác định của hàm số đó.
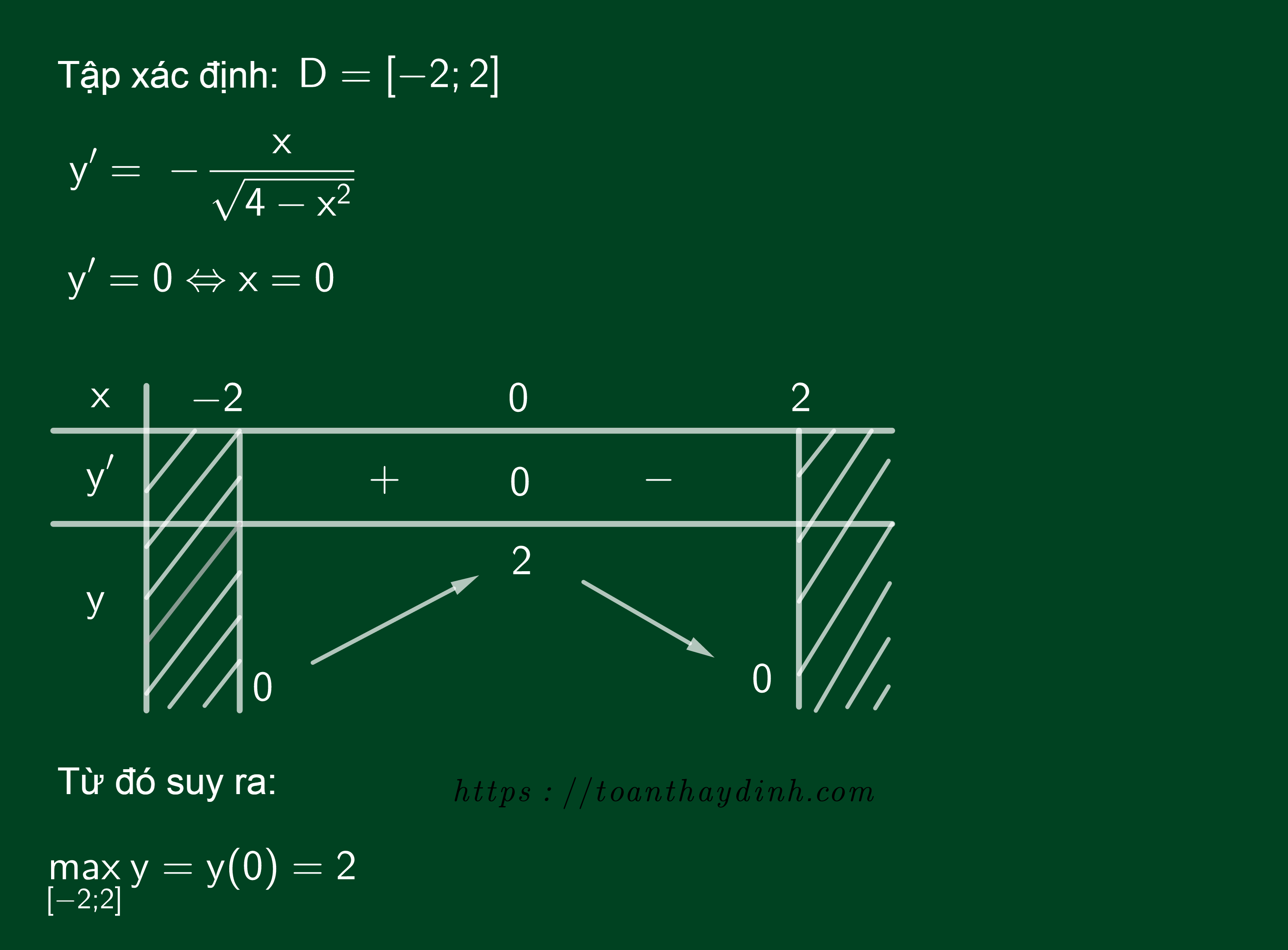
Ví dụ:
Tìm giá trị lớn nhất của hàm số .
Lời giải:
Tìm gtln gtnn của hàm số chứa căn lớp 12
Đề thi Online có giải:
[5-6] Xác định GTNN-GTLN của hàm số trên khoảng (a;b)
[5-6] Xác định GTNN-GTLN của hàm số trên đoạn
[5-6] Xác định GTNN_GTLN của hàm số thông qua đồ thị, bảng biến thiên
TÌM GIÁ TRỊ LỚN NHẤT NHỎ NHẤT CỦA HÀM SỐ BẰNG MÁY TÍNH
Tìm giá trị lớn nhất của hàm số, tìm giá trị nhỏ nhất của hàm số bằng Casio thường được sử dụng trong thi trắc nghiệm toán. Phương pháp này tỏ ra khá hữu hiệu trong các bài toán đơn giản như không có tham số, khoảng đoạn được xét ngắn. Để sử dụng chúng ta khai thác chức năng TABLE của máy tính bỏ túi.
Ví dụ:
Gọi M,m lần lượt là gtln,gtnn của hàm số . Tính tích Mm.
A. 1.
B. 1/8.
C. -3/8.
D. 1/8.
Lời giải:
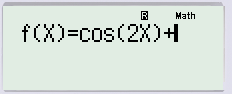
Mở chức năng TABLE trong máy tính (chế độ 1 hàm số, đơn vị góc Radian). Nhập vào hàm số .
Ở mục START chúng ta chọn 0, ở mục END chúng ta chọn 2π (Lý do chọn như vậy là vì chu kỳ hàm số này không quá 2π) , ở mục STEP chúng ta chọn 2π/19.
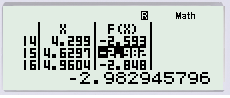
Ở cột F(X) ta dò được giá trị gần với GTNN là −2.982 (Giá trị này càng chính xác nếu STEP càng nhỏ).
Tương tự ta cũng dò được giá trị gần với GTLN là 0.114.
Từ đó so sánh ta chọn được đáp án C.
Chúc các em thành công!
Hàm số -