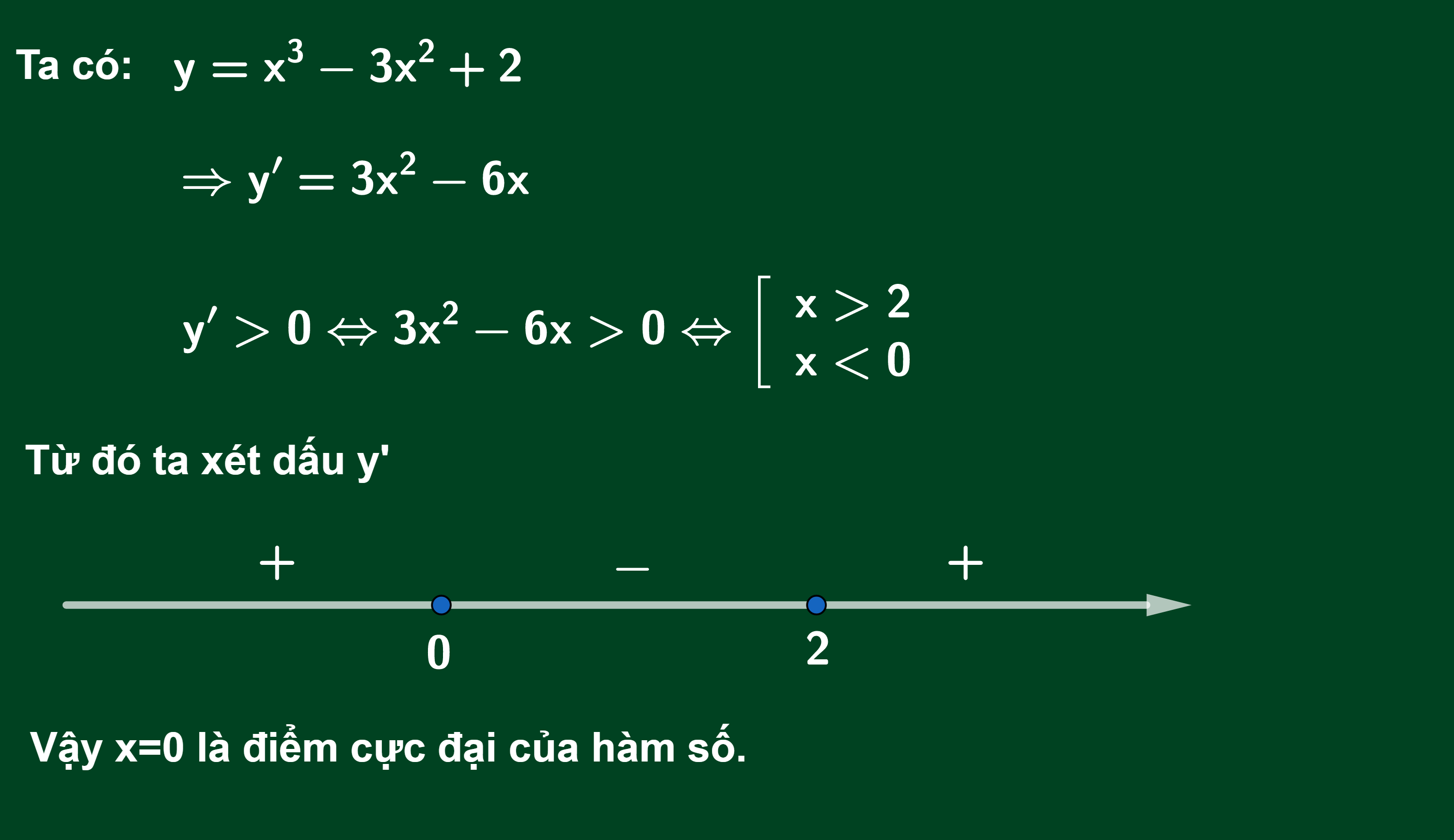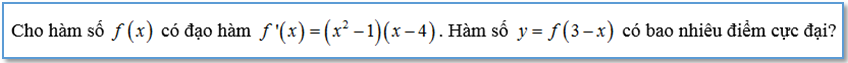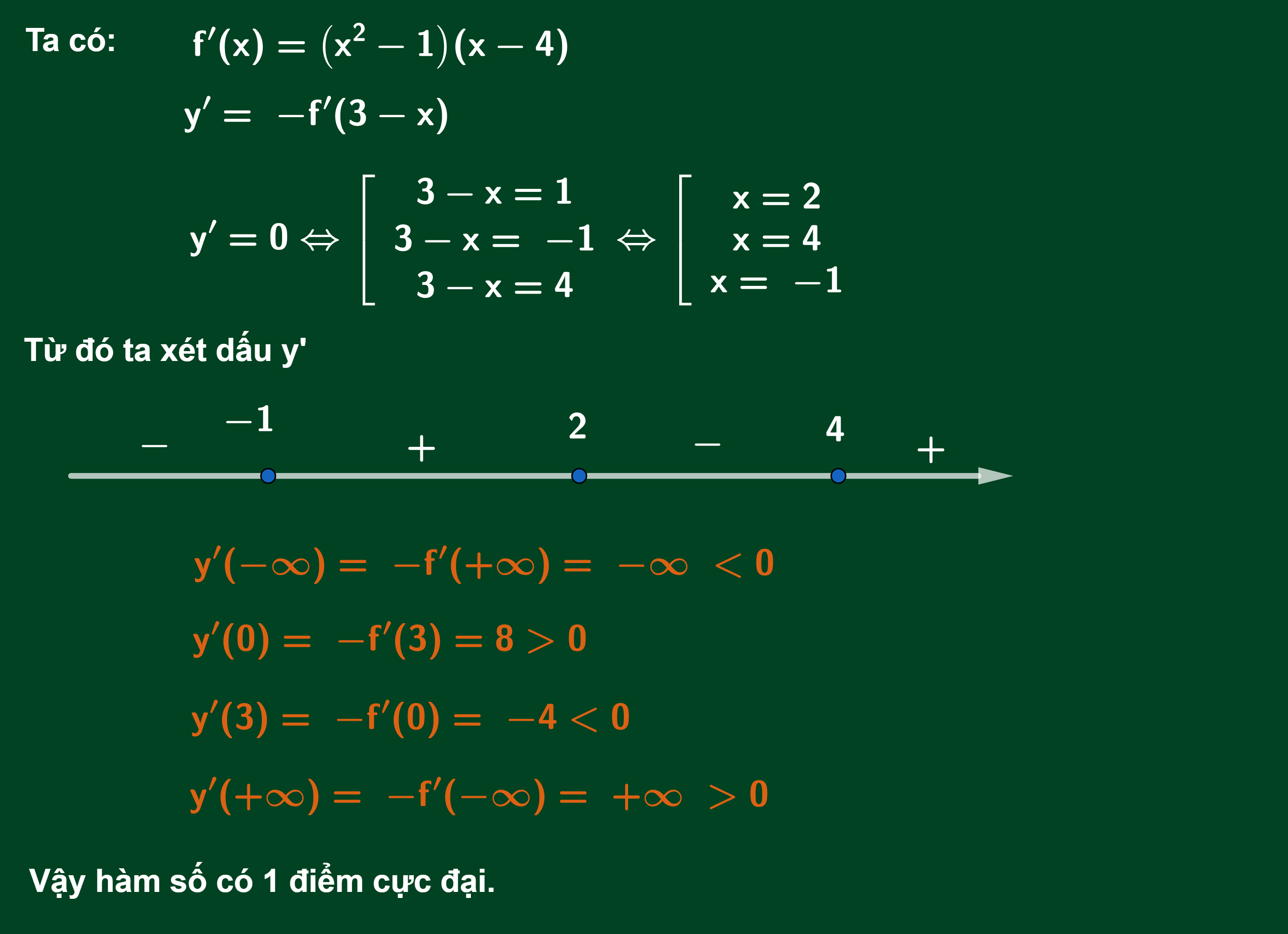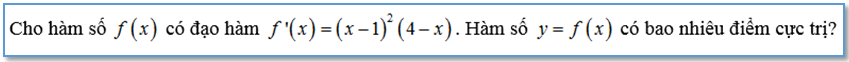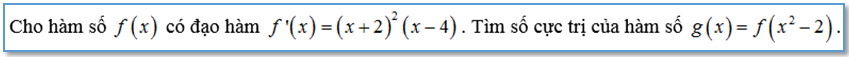Ba phương pháp xét dấu đạo hàm tìm cực trị của hàm số
Bài viết dưới đây tôi sẽ hướng dẫn các bạn tìm hiểu khái niệm và 3 phương pháp tìm CỰC TRỊ CỦA HÀM SỐ.
Content
I. CỰC TRỊ CỦA HÀM SỐ LÀ GÌ?
Bài viết này nêu định nghĩa hơi khác SGK một chút. Các bạn chú ý sách giáo khoa định nghĩa cực trị cho hàm liên tục. Tuy nhiên chúng ta bỏ điều kiện liên tục thì đó vẫn là định nghĩa cho cực trị. Vì vậy ở đây tôi bỏ điều kiện liên tục cho tư duy của chúng ta rộng mở hơn nhé!.
Cho hàm số y=f(x) xác định trên khoảng (a;b) (a, b có thể là vô cực) và điểm α thuộc (a;b).
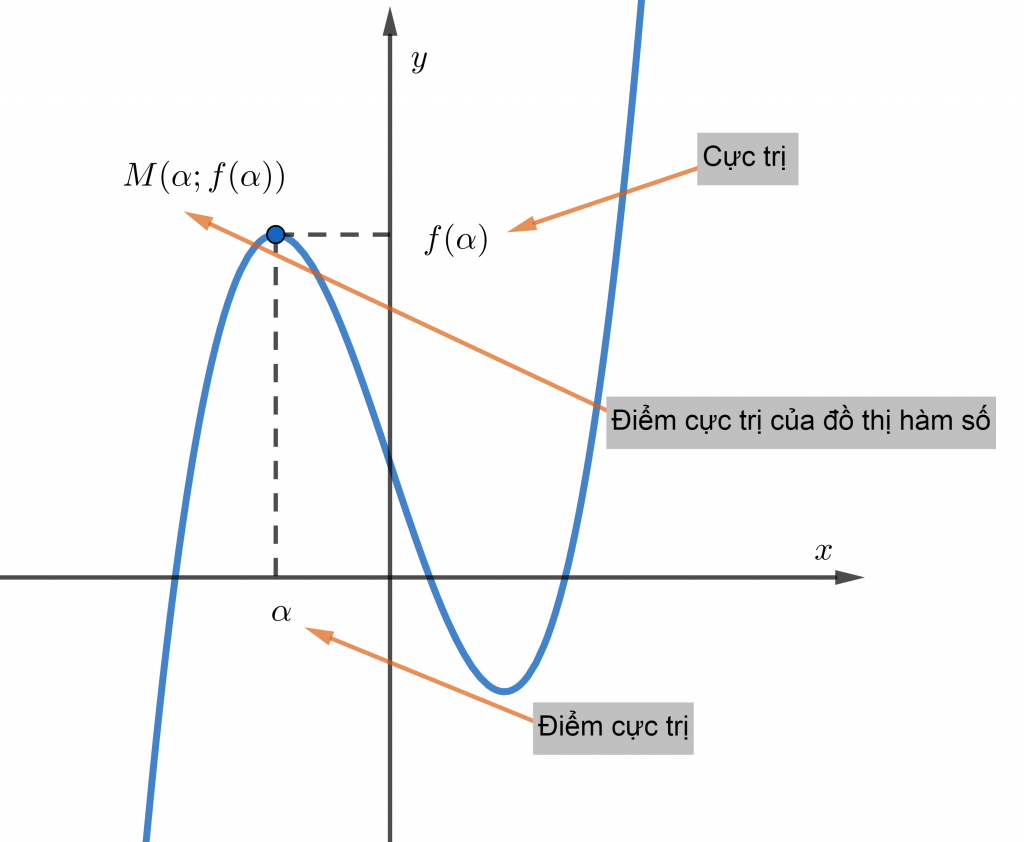
Nếu tồn tại một lân cận của điểm α trên khoảng (a;b) (lân cận của α là một khoảng nằm trong (a;b) và chứa điểm α) sao cho f(α)>f(x) với mọi giá trị x trên lân cận đó trừ đi điểm α. Thì f(α) là cực đại ( giá trị cực đại) của hàm số y=f(x). Và α được gọi là điểm cực đại của hàm số y=f(x). Điểm M(α;f(α)) được gọi là điểm cực đại của đồ thị hàm số y=f(x).
Hoàn toàn tương tự: Nếu tồn tại một lân cận của điểm α trên khoảng (a;b) sao cho f(α)<f(x) với mọi giá trị x trên lân cận đó trừ đi điểm α. Thì f(α) là cực tiểu ( giá trị cực tiểu) của hàm số y=f(x). Và α được gọi là điểm cực tiểu của hàm số y=f(x). Điểm M(α;f(α)) được gọi là điểm cực tiểu của đồ thị hàm số y=f(x).
Ta có thể so sánh với ví dụ:“Bạn là người lùn nhất (cao nhất) trong lớp nhưng bạn không phải người lùn nhất (cao nhất) trong trường học của bạn”. Cực trị hàm số cũng như vậy, nó mang tính chất “địa phương” chứ không mang tính chất “toàn cục”. Cực trị hàm số tại một điểm là giá trị nhỏ nhất hay lớn nhất trên một lân cận đủ nhỏ của điểm đó.
Về mặt đồ thị hàm số thì cực trị hàm số có thể được hiểu như là “đỉnh” hay “đáy” ở một khu vực đủ nhỏ.
II. PHÂN BIỆT MỘT SỐ KHÁI NIỆM
Từ định nghĩa trên ta lưu ý phân biệt mấy khái niệm sau:
III. PHƯƠNG PHÁP TÌM CỰC TRỊ CỦA HÀM SỐ CÓ ĐẠO HÀM
Các bạn lưu ý 2 định lý dưới đây có điều kiện hàm liên tục nhé. Và hãy rộng suy nghĩ xem nếu nó không liên tục tại α thì sẽ như thế nào.
Định lý 1:
Cho hàm số y=f(x) xác định, liên tục trên (a;b) và có đạo hàm trên một lân cận của α trên (a;b) có thể trừ điểm α.
Nếu tồn tại một lân cận của α trên (a;b) sao cho qua điểm α mà f'(x) đổi dấu từ dương sang âm thì hàm số f(x) đạt cực đại tại điểm α.
Nếu tồn tại một lân cận của α trên (a;b) sao cho qua điểm α mà f'(x) đổi dấu từ âm sang dương thì hàm số f(x) đạt cực đại tại điểm α.
Định lý 2:
Cho hàm số y=f(x) xác định, liên tục trên (a;b) và có đạo hàm đến cấp 2 trên một lân cận của α trên (a;b) có thể trừ điểm α.
Nếu f'(α)=0 và f”(α)>0 thì hàm số f(x) đạt cực tiểu tại α.
Nếu f'(α)=0 và f”(α)<0 thì hàm số f(x) đạt cực đai tại α.
Nếu f'(α)=0 và f”(α)=0 thì ta chưa xét được cực trị tại α. Trong trường hợp này hàm số có thể đạt (ví dụ hàm số y=x^4)hoặc không đạt cực trị (ví dụ hàm số y=x³).
Từ hai định lý trên ta có hai cách để xét cực trị. Với định lý 1 ta xét cực trị bằng cách xét dấu của đạo hàm. Với định lý 2 ta xét cực trị bằng cách xét đến đạo hàm cấp 2. Mỗi phương pháp đều có ưu nhược điểm riêng. Tùy bài toán chúng ta cần vận dụng phù hợp.
Bộ đề thi Online các dạng có giải chi tiết: Cực trị Hàm số
IV. PHƯƠNG PHÁP XÉT DẤU ĐẠO HÀM ĐỂ TÌM CỰC TRỊ CỦA HÀM SỐ
Các nhận xét dưới đây đều dành cho hàm số có đạo hàm liên tục.
1. GIẢI BẤT PHƯƠNG TRÌNH f'(x)>0.
Nói cho dễ hiểu thì khi giải được bất phương trình f'(x)>0 thì những giá trị còn lại không thuộc miền nghiệm của f(x)>0 sẽ thỏa mãn f(x)≤0. Như vậy là ta đã xét được dấu của đạo hàm rồi.
Ví dụ 1:
Lời giải:
Ví dụ2:
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Cực trị Hàm số
2. GIẢI f'(x)=0 SAU ĐÓ THỬ GIÁ TRỊ f'(x) ĐỂ XÉT DẤU
Nói cho dễ hiểu: Nếu f'(x) liên tục trên (a;b), f'(a)=f'(b)=0 và f'(x)≠0 với mọi x∈(a;b) thì f'(x) đồng dấu trên khoảng (a;b).
Ví dụ 1:
Lời giải:
Ví dụ 2:
Lời giải:
3. XÉT DẤU ĐẠO HÀM THEO BỘI CỦA NGHIỆM
Ví dụ 1:
Lời giải:
Ví dụ 2:
Lời giải:
Trên đây là ba phương pháp xét dấu của đạo hàm để giải quyết bài toán cực trị hàm số. Mỗi phương pháp đều có ưu điểm và nhược điểm. Đối với giải toán TN chúng ta nên ưu tiên phương pháp thứ hai để tiết kiệm thời gian. Với học sinh khá giỏi ta nên làm theo phương pháp thứ ba. Tại sao lại như vậy? Với kinh nghiệm của bản thân mình cho thấy học sinh chưa hiểu nguyên lý xét dấu theo bội của nghiệm thường không phân biệt được số bội. Chúc các bạn học giỏi, thành công!
Bộ đề thi Online các dạng có giải chi tiết: Hàm số
Bài tập Online có giải: Cực trị của Hàm Số
Xem thêm: Giá trị lớn nhất nhỏ nhất của hàm số
Xem thêm: Tìm m để hàm số không có cực trị như thế nào?
Xem thêm: Bài tập trắc nghiệm cực trị của hàm số
Xem thêm: Tìm m để hàm số có cực trị (hàm số đa thức bậc 3)
Xem thêm: Tìm m để hàm số có 3 cực trị (hàm số trùng phương)
Hàm số -