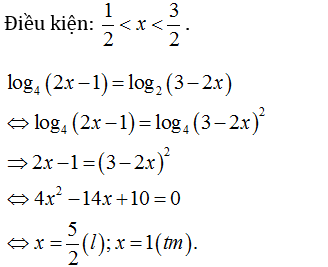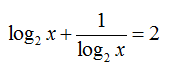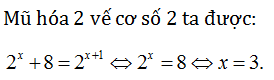Một số phương pháp giải phương trình logarit

Bài viết dưới đây tổng hợp các phương pháp giải phương trình logarit như: Đưa về cùng cơ số; Đặt ẩn phụ; Mũ hóa; Đánh giá. Trong mỗi phương pháp đều có 1 ví dụ minh họa. Các bạn cùng theo dõi nhé.

Content

1. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT BẰNG CÁCH ĐƯA VỀ CÙNG CƠ SỐ

Các bạn lưu ý rằng trong quá trình biến đổi phương trình logarit mà ta không theo dõi được miền xác định thi ta nên đặt diều kiện trước khi biến đổi. Còn trong quá trình biến đổi ta vận dụng các công thức mũ và logarit đã biết để biến đổi. Sau khi giải ra được x thì ta cần kiếm tra lại điều kiện để có kết quả nghiệm.

Ví dụ: Giải phương trình sau

phương pháp giải logarit

Ta thấy ở cơ số ở hai vế khác nhau nhưng 2²=4 nên có thể đưa về cùng cơ số 2 hoặc cơ số 4.

Lời giải:

phương pháp giải toán logarit

Vậy phương trình đã cho có nghiệm duy nhất x=1.

Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit

2. GIẢI PHƯƠNG TRÌNH LOGARIT BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ

Trong một số phương trình logarit việc đặt ẩn phụ có thể đưa đến phương trình đơn giản hơn như phương trình bậc 2, bậc 3. Vì hàm logarit có miền giá trị là R nên đặt t=log_a{x} thì không cần điều kiện của t.

Ví dụ: Giải phương trình sau

giải phương trình logarit bằng cách đặt ẩn phụ

Nếu các bạn đã làm quen dạng toán này thì ta có thể bỏ qua bước đặt ẩn phụ để biến đổi tương đương. Còn với các bạn mới bắt đầu thì ta hãy cứ làm đủ các bước để hiểu đã nhé.

Lời giải:

phương pháp giải phương trình logarit

Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit

3. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT BẰNG CÁCH ĐÁNH GIÁ 2 VẾ

Trong một số phương trình không mẫu mực ta có thể sử dụng phương pháp đánh giá 2 vế để giải. Cụ thể nếu phương trình có dạng A=B mà ta đánh giá được A≤C còn B≥C thì phương trình có nghiệm tại các điểm đạt dấu =.

Ví dụ: Giải phương trình sau

Lời giải:

4. GIẢI PHƯƠNG TRÌNH LOGARIT BẰNG PHƯƠΝG PΗÁP MŨ HÓA

Với một số phương trình ta có thể mũ hóa để đưa về phương trình mũ đơn giản hơn.

Ví dụ: Giải phương trình sau

Lời giải:

Trên đây là một số cách giải phương trình logarit thường thấy ở bậc THPT. Chúc các bạn thành công!

Đề thi các dạng có Giải chi tiết Phương trình Mũ – Logarit

Bài tập mức độ [5 – 8] điểm Bài tập mức độ [7-8] điểm Bài tập mức độ [9-10] điểm
[5-6] PT mũ – Phương trình cơ bản [7-8] Phương trình logarit – Dạng đặt ẩn phụ
[9-10] Phương trình mũ chứa tham số
[5-6] PT mũ – Biến đổi đưa về dạng cơ bản [7-8] Phương trình logarit – Dạng đưa về cùng cơ số [9-10] Phương trình logarit chứa tham số
[5-6] PT Logarit – Phương trình cơ bản [7-8] Phương trình logarit – Dạng hàm số, đánh giá [9-10] Phương trình kết hợp của mũ và logarit chứa tham số
[5-6] PT Logarit – Biến đổi đưa về phương trình cơ bản [7-8] Phương trình logarit – Dạng mũ hóa
[7-8] Phương trình mũ – Dạng đặt ẩn phụ
[7-8] Phương trình mũ – Dạng đưa về cùng cơ số
[7-8] Phương trình mũ – Dạng hàm số, đánh giá
[7-8] Phương trình mũ – Dạng logarit hóa
[7-8] Phương trình tổ hợp mũ và logarit

 

Lũy Thừa - Lôgarit -