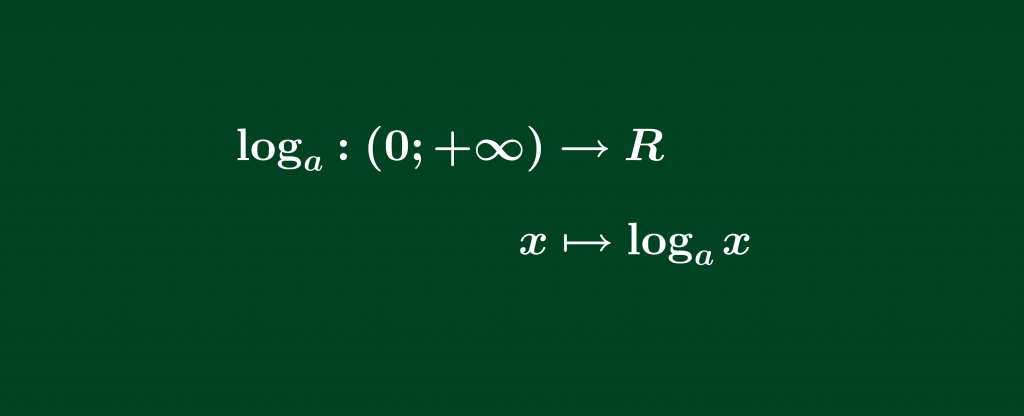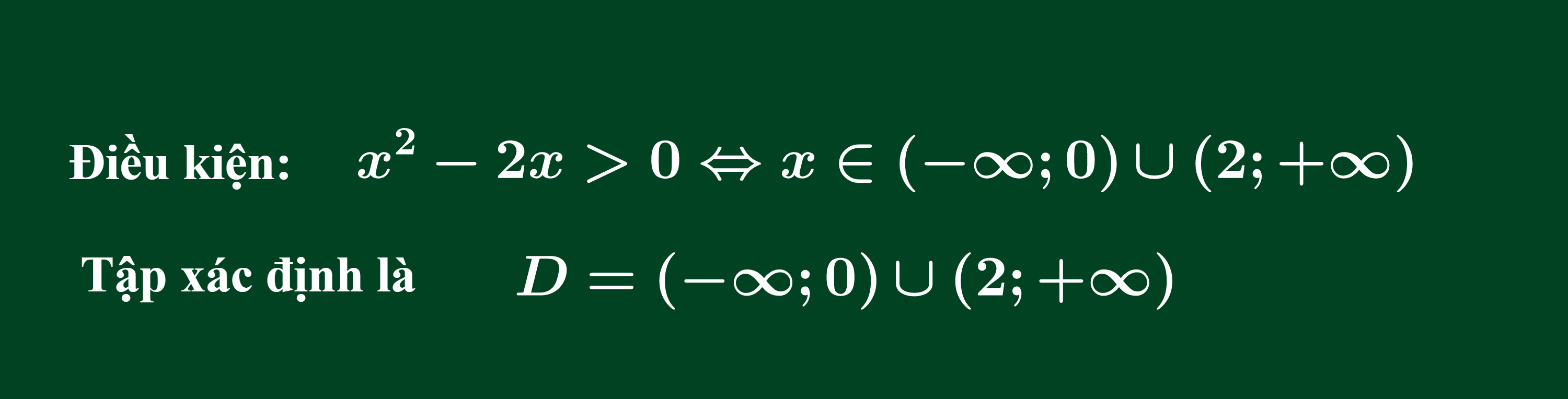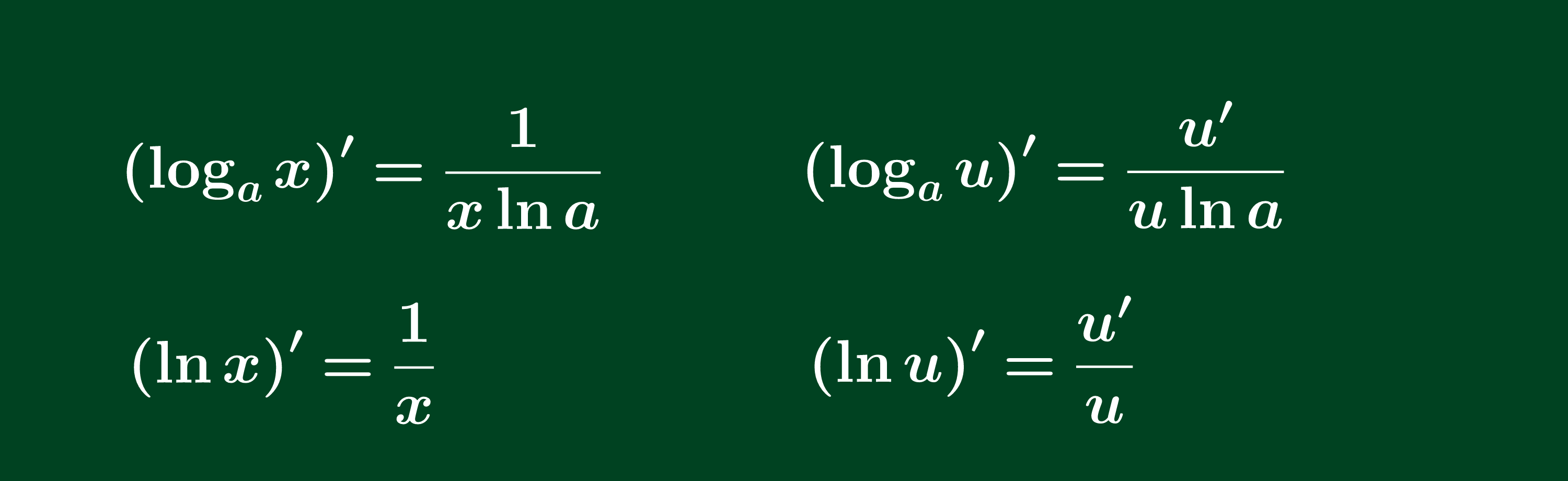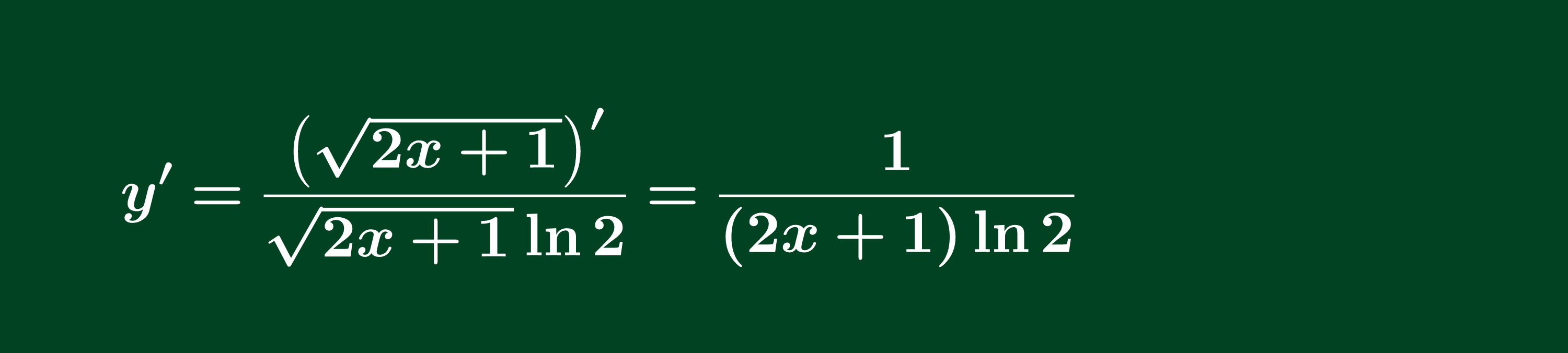Hàm số logarit: Định nghĩa và đồ thị

Bài viết dưới đây tôi sẽ giới thiệu tới các bạn hàm số logarit và các khái niệm liên quan. Các khái niệm liên quan đến nội dung này bao gồm: Định nghĩa; Tập xác định; Đạo hàm; Sự biến thiên; Đồ thị; Đường tiệm cận của đồ thị hàm số lôgarit.

ĐỊNH NGHĨA HÀM SỐ LOGARIT

Với cơ số a dương và khác 1, hàm số logarit cơ số a được định nghĩa như sau:

Như vậy chúng ta có thể thấy hàm số lôgarit xác định với mọi giá trị x dương. Và miền giá trị của hàm lôgarit là R

CÁCH TÌM TẬP XÁC ĐỊNH

Xem thêm:  Cách tìm tập xác định của hàm số loogarit

Với cơ số a dương và khác 1, từ định nghĩa ta thấy điều kiện xác định của hàm số lôgarit là u(x)>0 và u(x) xác định.

Ví dụ:

Tìm tập xác định của hàm số sau

Lời giải:

Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit

ĐẠO HÀM CỦA HÀM SỐ LOGARΙT

Đạo hàm của hàm số loga được cho bởi công thức:

Ví dụ:

Tính đạo hàm của hàm số sau

Lời giải:

ĐỒ THỊ HÀM SỐ LOGARIT

Theo phần đạo hàm bên trên ta có thể suy ra:

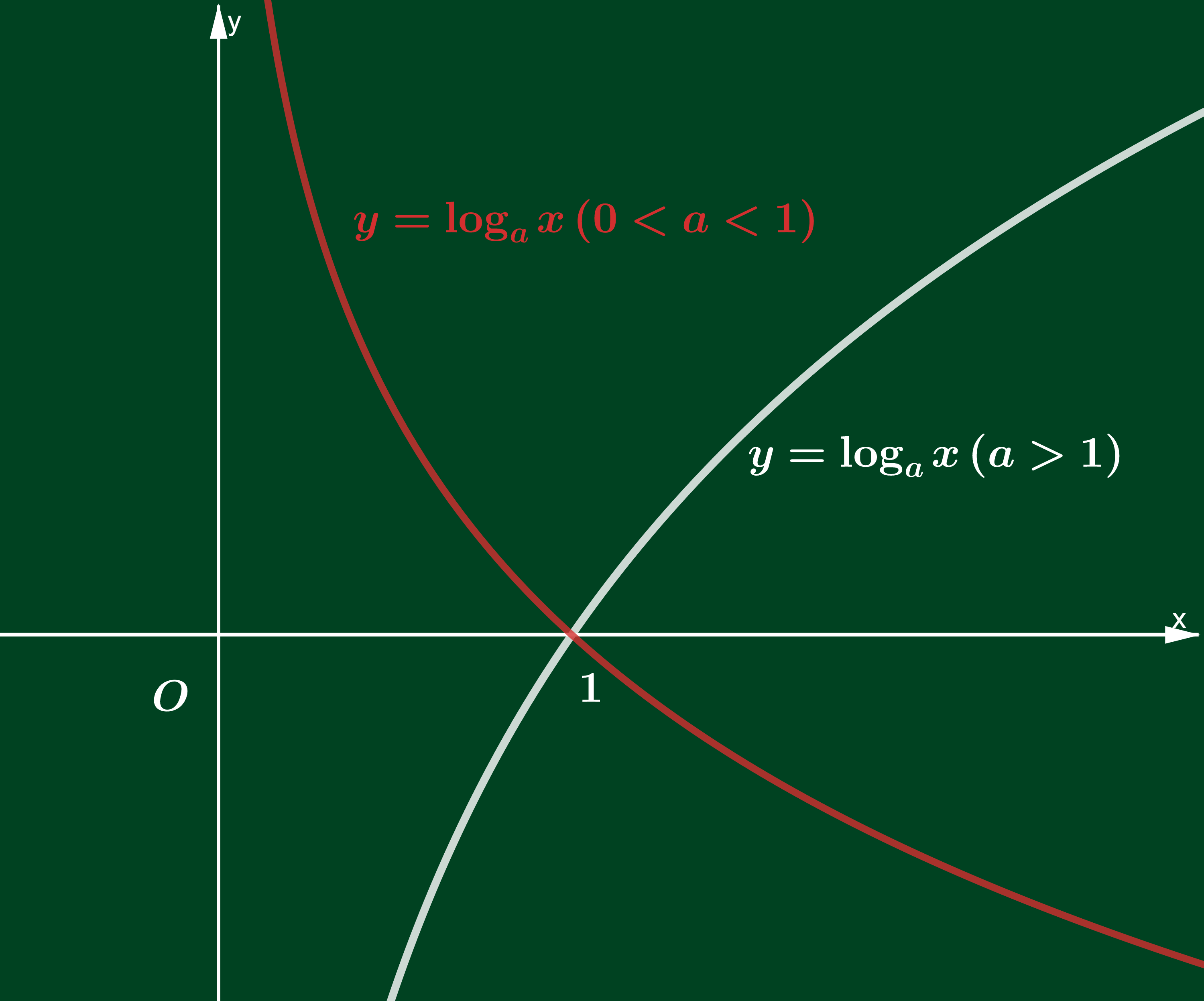
• Nếu cơ số lớn hơn 1 thì hàm số đồng biến trên miền xác định.
• Nếu cơ số dương và nhơ hơn 1 thì hàm số nghịch biến trên miền xác định.

Trong cả hai trường hợp đồ thị đều có 1 đường tiệm cận đứng là trục hoành và luôn luôn đi qua điểm I(1;0).

Dưới đây là hình minh họa cho hai trường hợp về đồ thị của hàm số lôga.

Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit

Trên đây là một số khái niệm liên quan đến hàm số loogarit. Chúc các bạn học giỏi và thành công!