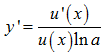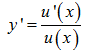Tổng hợp công thức đạo hàm logarit mũ đầy đủ

Cảm ơn các bạn đã ghé thăm blog. Bài viết này tổng hợp các công thức đạo hàm logarit và mũ giúp các bạn tra cứu nhanh nhất.

1. CÔNG THỨC TÍNH ĐẠO HÀM LOGARIT

Cho hàm số y=log_ax. Khi đó đạo hàm của hàm số trên là:

đạo hàm logarit

Trường hợp tổng quát hơn, cho hàm số y=log_au(x). Đạo hàm là:

công thức đạo hàm logarit

Ví dụ:

Tính đạo hàm của hàm số y=log_2(x^2+x+1).

Lời giải:

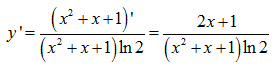
đạo hàm logarit cơ số xTrường hợp đặc biệt, khi cơ số của hàm logarit là e. Hay y=lnx. Ta có công thức đạo hàm như sau:

đạo hàm lnxNếu y=lnu(x) thì ta có:

đạo hàm hàm hợp

Đề thi Online có giải: Đề [7-8 điểm] Tính đạo hàm – Mũ – Logarit

Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit

2. CÔNG THỨC TÍNH ĐẠO HÀM MŨ

Cho hàm số y=a^x. Đạo hàm của hàm số là:

Trường hợp tổng quát hơn,  y=a^u(x). Ta có:

Ví dụ:

Tính đạo hàm của hàm số y=2^(x^2+x+1).

Lời giải:

đạo hàm hàm mũ

Đặc biệt, nếu cơ số của hàm mũ là e. Hay y=e^x. ta có công thức:

đạo hàm của e mũ xTa thấy đây là hàm số mà ta đạo hàm bao nhiêu lần thì hàm số cũng không thay đổi.

Nếu y=e^u(x) thì ta có công thức:

Trên đây là toàn bộ công thức tính đạo hàm logarit và mũ. Để tiện lợi cho các bạn lưu lại để học tôi sẽ tổng hợp lại trong bảng công thức tính đạo hàm logarit mũ sau đây:công thức đạo hàm logarit mũ đầy đủ

Trong các công thức trên thì công thức số 4 và số 8 là 2 công thức tổng quát. Các bạn nhớ 2 công thức này là có thể tự suy ra các công thức còn lại. Chẳng hạn chúng ta chỉ cần lưu ý (x)’=1. Khi đó các bạn thay u=x vào các công thức 4 và 8 là ta thu được công thức 3 và 7. Hay khi các bạn thay a=e, thay u=x thì các bạn được công thức 1 và 5. Khi các bạn thay a=e thì ta được công thức 2 và 6. Thật đơn giản phải không nào! Chúc các bạn học tập vui vẻ!

Lũy Thừa - Lôgarit -