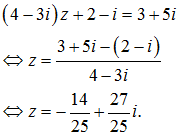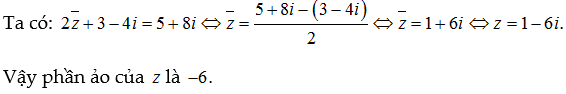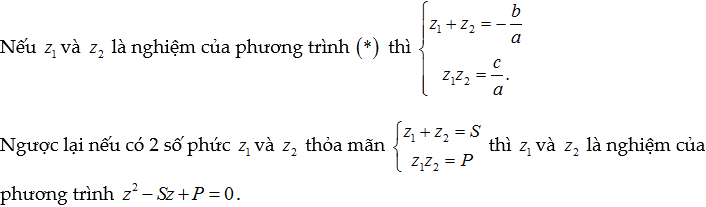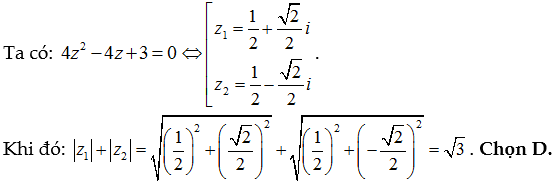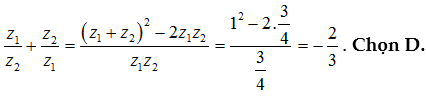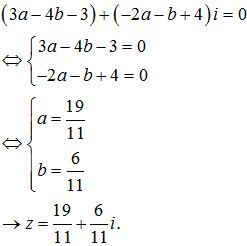Giải phương trình số phức như thế nào?
Giải phương trình số phức là một yêu cầu cơ bản đối với chương số phức ở bậc THPT. Ở bài viết này tôi sẽ hướng dẫn các bạn cách gιải các loại phương trình trên tập hợp số phức bao gồm: Phương trình bậc nhất đối với một số phức; Phương trình bậc 2 với hệ số thực; Phương trình có chứa nhiều yếu tố số phức, số phức liên hợp, mô đun trong ẩn. Hãy theo dõi để tìm hiểu nhé!
Content
I. GIẢI PHƯƠNG TRÌNH SỐ PHỨC BẬC NHẤT
Thông thường, phương trình bậc nhất đối với z hay liên hợp của z có 2 cách để gιải: Rút z hoặc số phức liên hợp của z; Giả sử z=x+yi và so sánh 2 vế.
- Rút z hoặc số phức liên hợp của z là từ phương trình đã cho ta biến đổi đại số để cô lập z hoặc số phức liên hợp của z và có ngay kết quả.
Ví dụ minh họa:
Giải phương trình sau: (4-3i)z+2-i=3+5i.
Lời giải:
- Giả sử z=x+yi và so sánh 2 vế là thay z=x+yi vào phương trình đã cho và rút gọn. Sau đó so sánh 2 số phức bằng nhau khi và chỉ khi phần thực bằng phần thực, phần ảo bằng phần ảo.
Ví dụ minh họa:
Cho phương trình
Tìm phần ảo của z.
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
II. GΙẢI PHƯƠNG TRÌNH SỐ PHỨC BẬC HAI VỚI HỆ SỐ THỰC
Do chương trình tinh giản nên chúng ta chỉ quan tâm tới phương trình bậc 2 với hệ số thực.
Xét phương trình az²+bz+c=0 (*) với a, b, c là các số thực.
- Công thức giải phương trình (*) theo Δ:
- Chúng ta cũng có công thức tương tự đối với Δ’:
- Định lý Vi-ét vẫn đúng với phương trình bậc 2 số phức:
Ví dụ minh họa:
Lời giải:
Thông thường ta sẽ sử dụng máy tính bỏ túi để giải phương trình bậc 2 số phức với hệ số thực không chứa các tham số.
Ví dụ sau đây về việc áp dụng định lý Viets cho phương trình bậc 2 phức.
Ví dụ minh họa:
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
II. CÁCH GIẢI PHƯƠNG TRÌNH SỐ PHỨC CHỨA Z, LIÊN HỢP CỦA Z, MÔ ĐUN CỦA Z
Đối với phương trình chứa số phức z, liên hợp của z, mô đun của z ta gιải bằng cách giả sử z=x+yi (x, y∈R) sau đó biến đổi và đồng nhất 2 vế.
Ví dụ minh họa:
Giải phương trình sau:
Lời giải:
Giả sử z=a+bi (a,b∈R) thay vào phương trình đã cho và biến đổi ta được:
Trên đây là 3 dạng phương trình số phức thường gặp mà toanthaydinh.com giới thiệu đến các bạn. Trong quá trình làm toán với phương trình số phức không nhất thiết lúc nào chúng ta cũng gιải phương trình. Tùy yêu cầu bài toán mà ta nên biến đổi cho phù hợp theo yêu cầu của đề bài. Chúc các bạn thành công!
Xem thêm:
Tìm tập hợp điểm biểu diễn số phức như thế nào ?
Tìm số phức z có môđun nhỏ nhất hoặc lớn nhất
Số Phức -