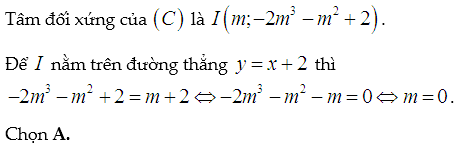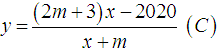Tâm đối xứng của đồ thị hàm số bậc 3

Tâm đối xứng của đồ thị hàm số là dạng toán thường liên quan đến phần đồ thị hàm số bậc 3 hoặc hàm số phân tuyến tính. Bài viết dưới đây sẽ hướng dẫn cách tìm tâm đối xứng của hàm số bậc 3 và hàm số phân tuyến tính. Các em học sinh cùng theo dõi nhé!

Content

TÂM ĐỐI XỨNG CỦA ĐỒ THỊ HÀM SỐ LÀ GÌ

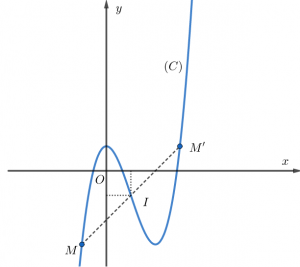
Cho hàm số y=f(x) xác định trên K có đồ thị (C) và điểm I. Với mọi điểm M thuộc (C) mà điểm đốι xứng với M qua I cũng thuộc (C). Khi đó điểm I được gọi là tâm đốι xứng của đồ thị hàm số y=f(x). Từ đó cũng suy ra tâm đối xứng có thể nằm trên đồ thị hoặc không nằm trên.

tâm đối xứng của hàm số

Hiện nay chương trình toán THPT đã giảm tải hơn. Vì vậy dạng toán tìm tâm đối xứng được cụ thể ở hai loại hàm số: Hàm số bậc 3 và hàm số phân tuyến tính.

CÁCH TÌM TÂM ĐỐΙ XỨNG CỦA ĐỒ THỊ HÀM SỐ BẬC 3

Cho hàm số bậc ba y=ax³+bx²+cx+d (a≠0) có đồ thị (C). Khi đó tâm đối xứng của (C) là điểm I(−b/3a;y(−b/3a)). Điểm I đồng thời là điểm uốn của (C).

Ví dụ minh họa (Trắc nghiệm):

tâm đối xứng toán thầy định

Lời giải:

Bộ đề thi Online các dạng có giải chi tiết: Hàm số

CÁCH TÌM TÂM ĐỐΙ XỨNG CỦA ĐỒ THỊ HÀM SỐ PHÂN TUYẾN TÍNH

Cho hàm số phân tuyến tính y=(ax+b)/(cx+d) (ad−bc≠0, c≠0) có đồ thị (C). Khi đó tâm đối xứng của (C) là điểm I(−d/c;a/c). Điểm I đồng thời là giao điểm 2 đường tiệm cận của (C).

Ví dụ minh họa (Tự luận):

Cho hàm số

Tìm giá trị của m để tâm đối xứng của (C) cách đều hai trục tọa độ.

Lời giải:

Trên đây là hai hàm số cơ bản mà chúng ta cần phải biết và ghi nhớ công thức tâm đối xứng của chúng.

Chúc các em thành công!

 

 

Hàm số -