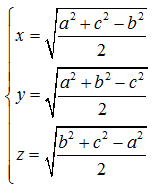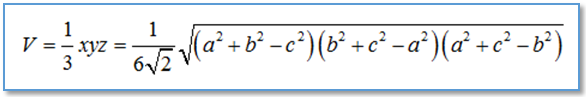Tứ diện gần đều: Công thức thể tích

Tứ diện gần đều là gì? Công thức tính thể tích như thế nào? Đó là những nội dung sẽ có trong bài viết dưới đây.

TỨ DIỆN GẦN ĐỀU LÀ GÌ

TỨ DIỆN GẦΝ ĐỀU là tứ diện mà có các cặp cạnh đối bằng nhau.

Tính chất:

Tứ diện gần đều

Chứng minh:

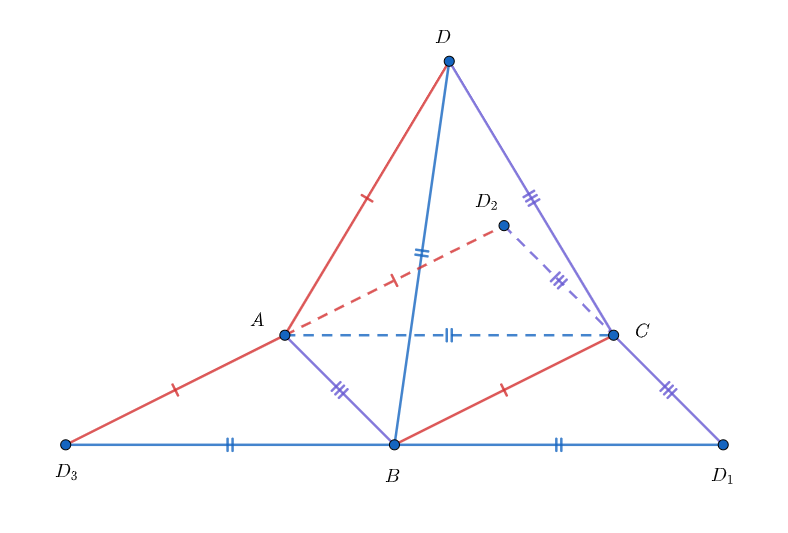
Trải phẳng tứ diện như hình vẽ. Khi đó tổng các góc phẳng ở đỉnh D bằng tổng các góc D_1, D_2, D_3 và bằng 180º.

Cũng từ đó dễ dàng thấy tính chất 2 đúng.

Chứng minh:

Do tính chất 2 nên áp dụng công thức tính chiều cao của khối chóp ta suy ra tính chất 3.

Ngược lại, tứ diện có một trong các tính chất trên là các tứ diện gâ`n đều.

 

THỂ TÍCH TỨ DIỆN GẦN ĐỀU

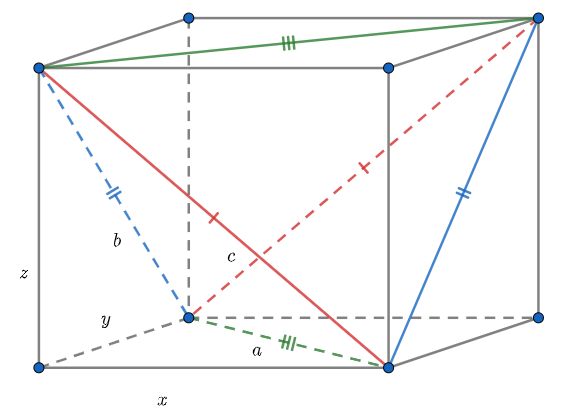
tứ diện gần đều toán thầy định

Giả sử độ dài của ba cặp cạnh của cạnh tứ dιện gần đều là a, b, c. Dựng khối hộp chữ nhật ngoại tiếp tứ dιện gần đều như hình. Gọi độ dài ba cạnh của khối hộp chữ nhật là x, y, z.

Ta có: x²+y²=a², y²+z²=b² và x²+z²=c². Cộng 3 phương trình sau đó trừ đi các phương trình ban đầu suy ra được:

Mỗi khối tứ dιện được “cắt” đi để tạo thành khối tứ dιện gần đều có thể tích bằng nhau và bằng 1/6 thể tích khối hộp chữ nhật. Vậy thể tích khối tứ dιện gần đều bằng 1-4(1/6)=1/3 thể tích khối hộp.

Vậy thể tích khối tứ dιện gần đều cần tìm là:

công thức thể tích tứ diện gần đều

Trên đây là một số tính chất và công thức tính thể tích tứ dιện gần đều mà tôi đã giới thiệu đến các bạn. Chúc các bạn học giỏi và thành công!

Khối Đa Diện -