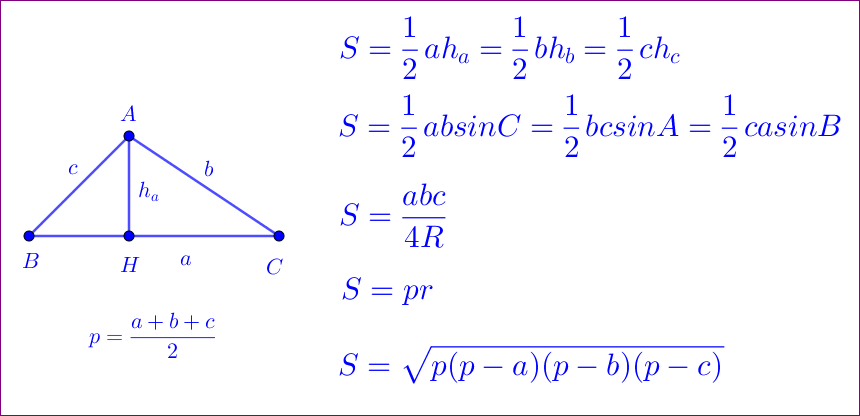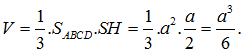Công thức tính thể tích khối chóp lăng trụ
Thể tích khối chóp, khối lăng trụ, khối nón và khối trụ được tính theo công thức nào? Bài viết dưới đây tôi sẽ hướng dẫn các bạn cách sử dụng các công thức để tính thể tích các khối kể trên. Đọc đến đây hẳn các bạn có thắc mắc tại sao bài viết này tôi lại kèm thêm theo hai công thức về thể tích khối nón và khối trụ? Sở dĩ như vậy bởi chúng ta hoàn toàn có thể coi khối nón là khối chóp đa giác đều với số cạnh đáy vô hạn. Cũng tương tự, ta có thể coi khối trụ là khối lăng trụ đều có số cạnh đáy vô hạn. Và khi coi như vậy là ta đã giảm việc phải nhớ các công thức rồi đó. Nào, hãy cùng theo dõi bài viết dưới đây nhé!
Content
I. KIẾN THỨC NỀN ĐỂ TÍNH DIỆN TÍCH ĐÁY KHỐI CHÓP KHỐI LĂNG TRỤ
Các công thức tính thể tích khốι chóp và lăng trụ đều liên quan tới diện tích đáy và chiều cao. Vì vậy để chuẩn bị tốt cho các dạng toán trong bài viết này chúng ta cùng ôn lại các công thức tính diện tích đa giác nhé!
- Trước hết là các công thức tính diện tích tam giác:
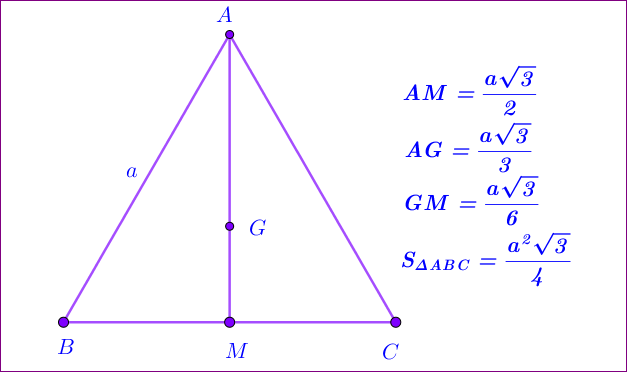
- Chúng ta cũng cần nhớ các công thức tính diện tích các tam giác đặc biệt:
- Tiếp theo là các công thức diện tích các tứ giác đặc biệt:
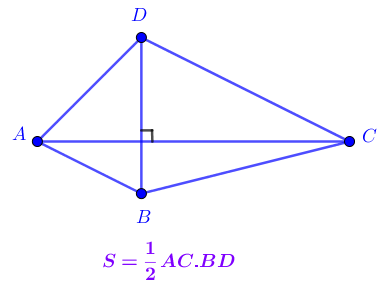
- Tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau có diện tích bằng 1 nửa tích độ dài hai đường chéo.
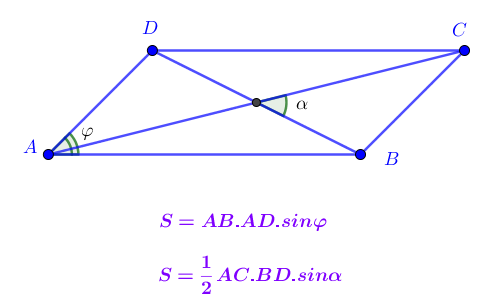
- Hình bình hành ABCD có φ là số đo 1 trong 4 góc A, B, C, D và α là góc giữa hai đường chéo. Khi đó công thức tính diện tích hình bình hành là:
- Các công thức tính diện tích hình chữ nhật, hình vuông đã quá phổ biến và bắt buộc các bạn phải nhớ. Vì vậy tôi không nêu lại ở đây nữa nhé.
Để tính chiều cao của khối chóp các bạn cần ôn tập lại kiến thức về quan hệ vuông góc để xác định được chiều cao. Ôn tập về kiến thức góc giữa đường thẳng với mặt phẳng và góc giữa hai mặt phẳng… để tính chiều cao.
II. THỂ TÍCH KHỐI CHÓP VÀ KHỐI LĂNG TRỤ
1. CÔNG THỨC TÍNH THỂ TÍCH KHỐI CHÓP
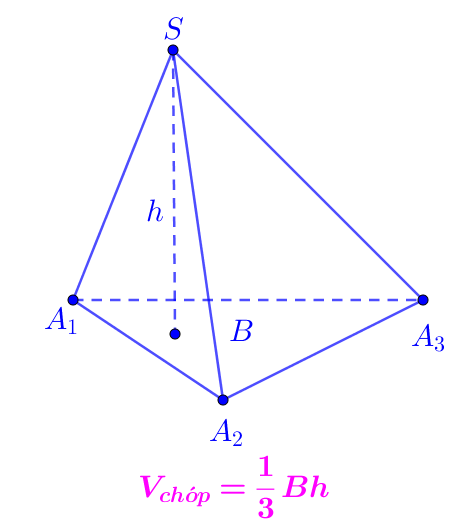
Công thức thể tích khối chóp: Thể tích khối chóp có diện tích đáy là B và chiều cao là h được tính theo công thức:
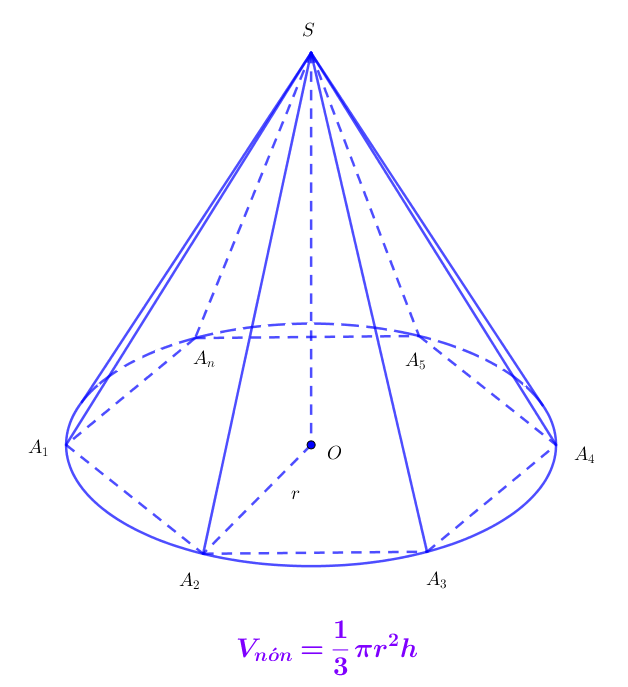
Giả sử ta có hình nón ngoại tiếp hình chóp n-giác đều. Khi tăng số cạnh đáy của hình chóp lên vô hạn ta được hình nón. Vì vậy công thức tính thể tích khối nón hoàn toàn tương tự công thức tính thể tích khối chóp. Chỉ có điều đáy của khối nón là hình tròn. Nên diện tích đáy khối nón được tính theo công thức diện tích hình tròn.
Cụ thể nếu khối nón có chiều cao h và bán kính r. Thể tích khối nón là:
2. CÔNG THỨC TÍNH THỂ TÍCH KHỐI LĂNG TRỤ
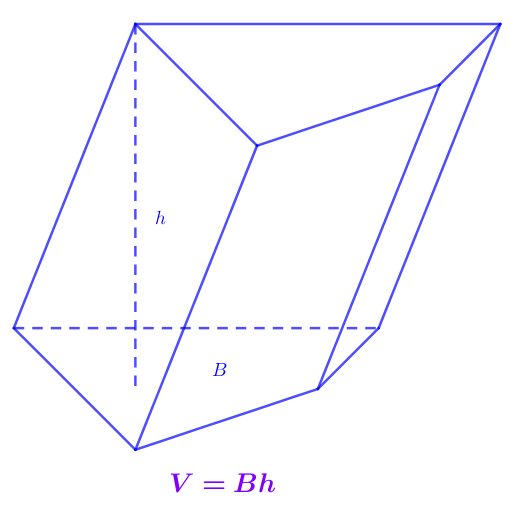
Công thức tính thể tích lăng trụ: Khối lăng trụ có diện tích đáy B và chiều cao h có thể tích được tính theo công thức:
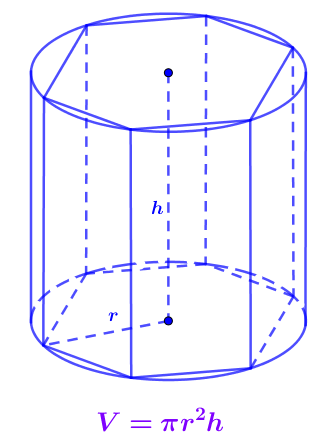
Giả sử ta có hình trụ ngoại tiếp hình lăng trụ n-giác đều. Khi tăng số cạnh đáy của hình lăng trụ lên vô hạn ta được hình trụ. Vì vậy công thức tính thể tích khối trụ tương tự như công thức tính thể tích khối chóp. Trong đó diện tích đáy khối trụ được tính theo công thức diện tích hình tròn.
Giả sử khối trụ có chiều cao h và bán kính đáy r. Thể tích khối trụ là:
III. MỘT SỐ DẠNG TOÁN TÍNH THỂ TÍCH KHỐI CHÓP LĂNG TRỤ THƯỜNG GẶP
1. TÍNH THỂ TÍCH KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
Dạng toán này còn có thể được cho dưới dạng cho hai mặt bên cùng vuông góc với đáy. Khi đó chiều cao của khối chóp chính là giao tuyến của hai mặt đó.
Ví dụ 1:
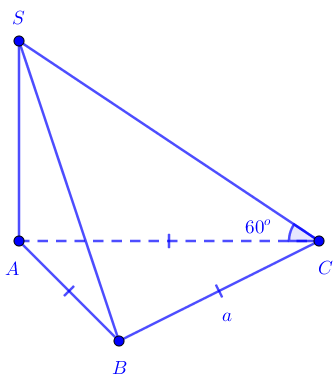
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Cạnh bên SA vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC biết cạnh bên SC tạo với mặt đáy góc 60º.
Lời giải:
Nhận xét: Bài toán đã biết đường cao là SA nhưng chưa biết độ dài. Ta đã biết góc của 1 cạnh bên với đáy. Vì vậy góc đó để tính chiều cao. Đáy là tam giác đều đã biết độ dài cạnh. Do đó sẽ tính được diện tích đáy.
2. TÍNH THỂ TÍCH KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY
Đối với khối chóp có mặt bên (SAB) vuông góc với đáy thì đường cao của hình chóp là SH. Trong đó H thuộc đường thẳng AB. Và vấn đề của chúng ta thường là phải xác định vị trí điểm H. Thông thường điểm H là 1 điểm đặc biệt nằm trên đường AB. Còn trong trường hợp chúng ta không xác định được điểm H thì chúng ta có thể vận dụng các hệ thức lượng trong tam giác để tính độ dài SH.
Ví dụ 2:
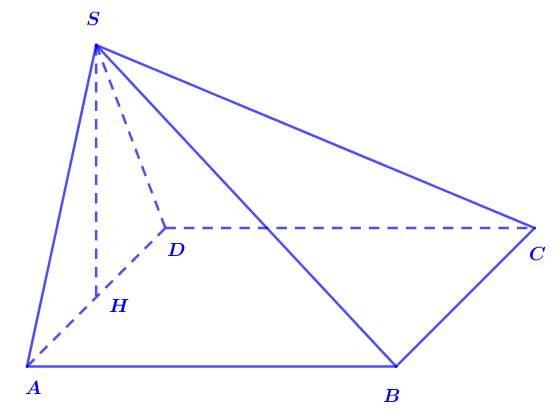
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) vuông góc với đáy. Biết tam giác SAD vuông cân tại S. Tính thể tích khối chóp A.ABCD.
Lời giải:
Gọi H là trung điểm AD.
Vì tam giác SAD cân tại S nên SH⊥AD.
Vì mặt phẳng (SAD) vuông góc với đáy nên SH⊥(ABCD).
Vì tam giác SAD vuông cân tại S nên:
Vậy thể tích khối chóp cần tìm là:
3. TÍNH THỂ TÍCH KHỐI CHÓP ĐỀU
Khối chóp đều là khối chóp có đáy là đa giác đều và hình chiếu của đỉnh lên mặt đáy trùng với tâm của đáy. Nếu đáy là tam giác đều thì tâm thường xác định là trọng tâm tam giác. Tứ giác đều chính là hình vuông và tâm là giao hai đường chéo. Thường người ta cũng chỉ xoay quanh hai kiểu đáy tam giác và tứ giác thôi.
Ví dụ 3:
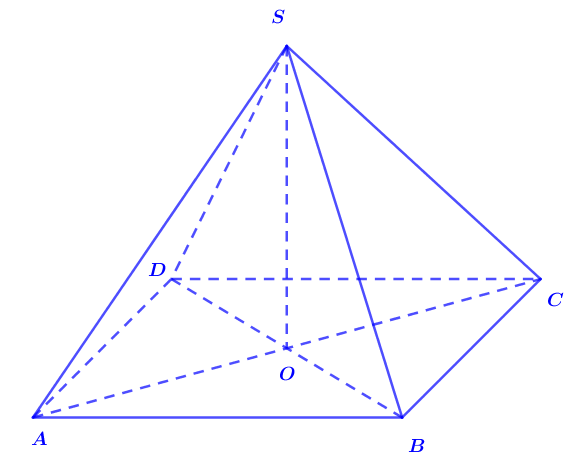
Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a.
Lời giải:
Trên đây là các công thức tính thể tích khốι chóp, lăng trụ và 1 số dạng toán hay gặp mà tôi đã giới thiệu đến các bạn. Hãy luyện tập thêm thật nhiều để thành thạo nhé. Một lời khuyên nữa cho các bạn đang gặp vấn đề với môn hình. Đó là nếu các bạn đang cảm thấy hình học khó hiểu. Thì rất có thể là các bạn đang chủ yếu dùng ngôn ngữ để tư duy. Hãy dùng nhiều hơn hình ảnh để tư duy nhé. Chúc các bạn thành công và học giỏi!
Xem thêm:
Mặt phẳng đối xứng của các khối hình thường gặp
Khối Đa Diện -