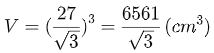Thể tích hình lập phương: Công thức và ví dụ
Trong bài viết dưới đây, tôi sẽ liệt kê các công thức liên quan đến thể tích hình lập phương để các bạn tiện tra cứu cho quá trình ôn tập. Vì trong bài viết này chúng ta quan tâm tới thể tích. Nên hai khái niệm hình lập phương và khối lập phương coi như tương đương nhau.
CÔNG THỨC TÍNH THỂ TÍCH HÌNH LẬP PHƯƠNG
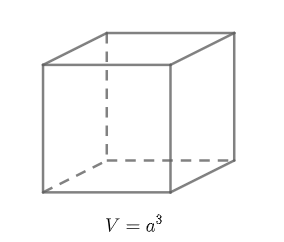
Hình lập phương là hình đa diện có tất cả các mặt là hình vuông.
Chúng ta có 1 số tính chất của hình lập phương cần quan tâm như:
- Hình lập phương là hình đa diện đều loại {4;3}. Mỗi mặt là hình vuông. Mỗi đỉnh là đỉnh chung của 3 mặt.
- Hình lập phương có 6 mặt, 8 đỉnh, 12 cạnh.
- Hình lập phương cạnh a có tổng diện tích các mặt là: S=6a².
- Hình lập phương cạnh a có độ dài đường chéo là
- Thể tích khối lập phương cạnh a là V=a³.
Ví dụ 1:
Cho khối lập phương cạnh a. Nếu tăng độ dài cạnh của khối lập phương lên 2 lần thì thể tích tăng lên mấy lần?
Lời giải:
Áp dụng công thức tính thể tích khối lập phương, ta có thể tích khối lập phương ban đầu là: V=a². Thể tích khối lập phương sau khi đã tăng độ dài cạnh lên 2 lần là: V’=(2a)³=8a³=8V. Vậy thể tích khối lập phương đã tăng lên 8 lần.
Ví dụ 2:
Tính thể tích khối lập phương có độ dài đường chéo bằng 27 cm.
Lời giải:
Độ dài cạnh của khối lập phương là
Vậy thể tích cần tìm của khối lập phương là
Ví dụ 3:
Cho khối lập phương có tổng diện tích các mặt là 24 (cm²). Hỏi thể tích của khối lập phương đó bằng bao nhiêu?
Lời giải:
Diện tích mỗi mặt của khối lập phương là 24:6=4 (cm²).
Vậy cạnh của hình lập phương là 2 (cm).
Do đó thể tích của khối lập phương đã cho là: 2³=8 (cm³).
Trên đây là công thức thể tích khối lập phương mà toanthaydinh.com giới thiệu đến các bạn. Chúc các bạn học giỏi và thanh công!
Khối Đa Diện -