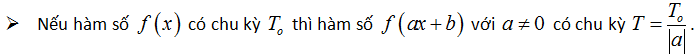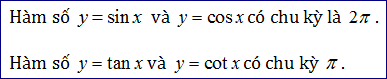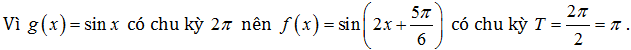Tìm chu kì của hàm số như thế nào?
Trong các loại hàm số có một loại hàm số có một tính chất đặc biệt. Đó là giá trị của hàm số được lặp lại sau một khoảng đều đặn. Gọi là hàm tuần hoàn. Bài viết này sẽ hướng dẫn các bạn – nhất là các bạn đang học phần hàm số lượng giác lớp 11 – cách để tìm chu kì của hàm số tuần hoàn.
CHU KÌ CỦA HÀM SỐ LÀ GÌ?
Trước hết ta hãy tìm hiểu khái niệm chu kỳ của hàm số. Giả sử hàm số f(x) xác định trên khoảng D nào đó. Và tồn tại T là một số thực dương sao cho:
- Với mọi x thuộc D thì x+T thuộc D.
- Với mọi x thuộc D thì f(x+T)=f(x).
Thì f(x) gọi là hàm tuần hoàn. Số thực T được gọi là chu kỳ của hàm số.
Chu kỳ nhỏ nhất được gọi là chu kỳ cơ sở (hay chu kỳ) của hàm số.
Trong chương trình toán phổ thông cơ bản thì không đề cập nhiều đến chu kỳ của hàm số. Nên trong bài viết này chúng ta hiểu là tìm chu kỳ của hàm số là chu kỳ nhỏ nhất. Và cũng chỉ xoay quanh tìm chu kỳ các hàm số lượng giác mà thôi.
MỘT SỐ CÔNG THỨC TÌM CHU KÌ CỦA HÀM SỐ LƯỢNG GIÁC
Dưới đây là một số công thức tìm chu kỳ hàm số lượng giác mà ta thường thấy. Trước hết, ta có định lý sau:
Định lý 1
Định lý 2
Ngoài ra, các hàm số lượng giác cơ bản có chu kỳ như sau:
Vận dụng vào một số ví dụ:
Ví dụ 1:
Tìm chu kỳ hàm số .
Giải:
Ví dụ 2:
Tìm chu kỳ hàm số .
Giải:
Ví dụ 3:
Tìm chu kỳ hàm số .
Giải:
Trên đây là một số lưu ý với các bạn khi xác định chu kỳ của một hàm số mà chủ yếu là hàm số lượng giác. Chúc các bạn học giỏi và thành công!
Xem thêm:
Lượng Giác -