Xét tính chẵn lẻ của hàm số lượng giác như thế nào?
Xét tính chẵn lẻ của hàm số lượng giác là một phần kiến thức Đai số 11. Bài viết giới thiệu tính chẵn lẻ bốn hàm số lượng giác cơ bản và một số gợi ý để xét tính chẵn lẻ của các hàm số lượng giác khác.
Phương pháp xét tính chẵn lẻ của hàm số có thể xem thêm tại đây.
Content
TÍNH CHẴN LẺ CỦA CÁC HÀM SỐ LƯỢNG GIÁC CƠ BẢN
Chúng ta có bốn hàm số lượng giác cơ bản là y=sinx, y=cosx, y=tanx, y=cotx.
a. Hàm số y=sinx
Tập xác định: R là tập đối xứng.
Vậy y=sinx là hàm số lẻ.
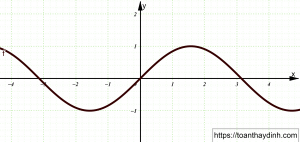
Đồ thị hàm số lượng giác y=sinx
b. Hàm số y=cosx
Tập xác định: R là tập đối xứng.
Vậy y=cosx là hàm số chẵn.
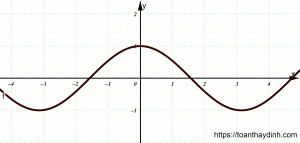
Đồ thị hàm số lượng giác y=cosx
c. Hàm số y=tanx
Tập xác định: là tập đối xứng.
Vậy y=tanx là hàm số lẻ.
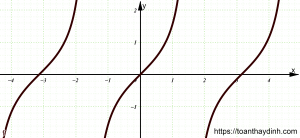
Đồ thị hàm số lượng giác y=tanx
d. Hàm số y=cotx
Tập xác định: là tập đối xứng.
Vậy y=cotx là hàm số lẻ.
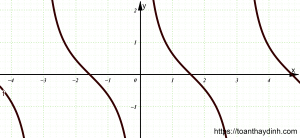
Đồ thị hàm số lượng giác y=cotx
Tóm lại, trong bốn hàm số lượng giác cơ bản chỉ có hàm số y=cosx là hàm số chẵn. Các hàm số còn lại là hàm số lẻ.
TÍNH CHẴN LẺ CỦA HÀM SỐ LƯỢNG GIÁC KHÁC
Với các hàm số lượng giác khác có thể tham khảo thêm cách xét tính chẵn lẻ của hàm số tại đây
Lưu ý thêm một số tính chất:
Tổng hoặc hiệu của hai hàm số chẵn (lẻ) là một hàm số chẵn (lẻ).
Tích hoặc thương hai hàm số chẵn (lẻ) là hàm số chẵn.
Tích hoặc thương một hàm số chẵn và một hàm số lẻ cùng xác định trên tập D là hàm số lẻ.
Chứng minh:
Ta chứng minh tổng của hai hàm số chẵn là một hàm số chẵn. Các trường hợp còn lại chứng minh hoàn toàn tương tự.
Giả sử f(x) và g(x) là hai hàm số chẵn có tập xác định lần lượt là .
Khi đó là tâp xác định của hàm số f(x)+g(x) cũng là tập đối xứng.
Hơn nữa: . Nên f(x)+g(x) là hàm số chẵn.
Áp dụng: Hàm số y=tanx+cotx là hàm số lẻ.
Chúc các em thành công!
Mọi đóng góp cho bài viết vui lòng để lại bình luận hoặc email.
Lượng Giác -
