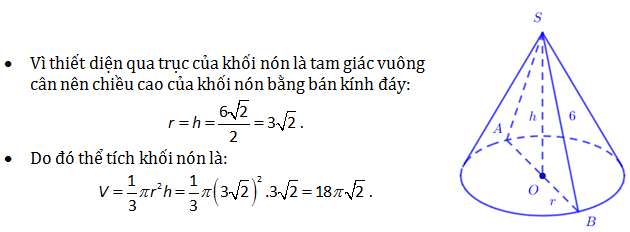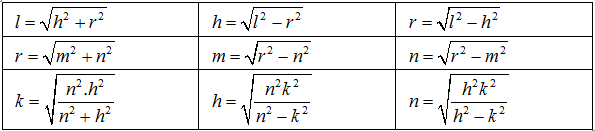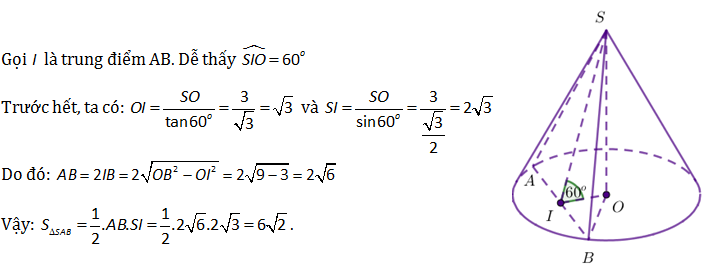Dạng toán thiết diện qua trục của hình nón
Trước hết cảm ơn tất cả các bạn đã ghé qua và đọc blog của mình! Hãy ghé qua blog thường xuyên để mình có động lực viết tiếp nhé! Với các bạn có mục tiêu 8+ hay 9+ môn Toán thì không thể bỏ qua dạng toán thiết diện qua trục của hình nón hay bài toán thiết diện hình nón nói chung. Bài viết này mình sẽ giới thiệu phương pháp cũng như cố gắng phân loại tất tần tật về các dạng toán này để các bạn dễ dàng học tập nhé!
Content
THIẾT DIỆN QUA TRỤC CỦA HÌNH NÓN LÀ GÌ
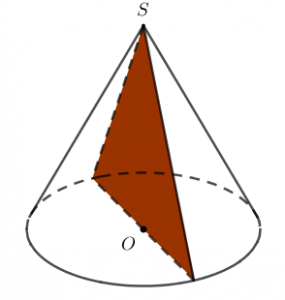
Cụ thể thì định nghĩa của nó như sau: Cho một hình nón (khối nón) có đỉnh S. Một mặt phẳng đi qua đỉnh S của hình nón và vuông góc với mặt đáy của hình nón đó sẽ cắt khối nón tương
ứng theo một hình tam giác. Hình tam giác đó được gọi là thiết diện qua trục của khối nón đó. (Xem hình vẽ)
Có thể dễ dàng thấy thiết diện qua trục của khối nón là một tam giác cân tại S. Có góc S chính là góc ở đỉnh của hình trụ. Đường cao của thiết diện ứng với đỉnh S chính là chiều cao hình nón. Hai cạnh bên của thiết diện là hai đường sinh.
DẠNG TOÁN VỀ THIẾT DIỆN QUA TRỤC CỦA KHỐI NÓN
Do định nghĩa bên trên nên bài toán về thiết diện qua trục của khối nón có thể xoay theo các hướng sau:
- Cho thông tin về khối nón. Tính diện tích hoặc thông tin kháccủa thiết diện.
- Cho thông tin về thiết diện. Tính các thông tin của khối nón.
Các bạn cùng theo dõi và luyện tập thông qua các ví dụ sau nhé:
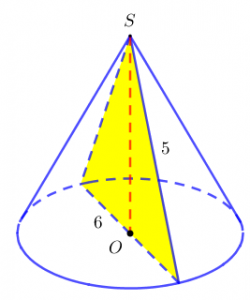
Ví dụ 1: Cho khối nón có đường kính đáy bằng 6 và độ dài đường sinh bằng 5. Tính diện tích thiết diện qua trục của khối nón đó.
Lời giải và hướng dẫn:
Với thông tin giả thiết như vậy thì khối nón đã xác định. Thứ còn thiếu để tính thiết diện là chiều cao. Ta có thể tính được dễ dàng thông qua định lý Pytago.
Chiều cao của khối nón là: 5²-3²=4.
Vậy diện tích của thiết diện là:(đvdt)
Ví dụ 2: Cho khối nón có thiết diện qua trục là tam giác vuông cân có cạnh góc vuông bằng 6. Tính thể tích khối trụ.
Lời giải và hướng dẫn:
Đây là bài toán cho thông tin của thiết diện qua trục và yêu cầu tìm 1 thông tin của khối trụ.
Qua 2 ví dụ này chắc các bạn cũng thấy OK rồi chứ. Tiếp theo chúng ta sẽ chuyển sang loại thiết diện “khó hơn” xíu. Đó là thiết diện qua đỉnh nhưng không qua trục của khối nón.
Bộ đề thi Online các dạng có giải chi tiết: Mặt Nón – Mặt Trụ – Mặt Cầu
DẠNG TOÁN VỀ THIẾT DIỆN KHÔNG QUA TRỤC CỦA HÌNH NÓN
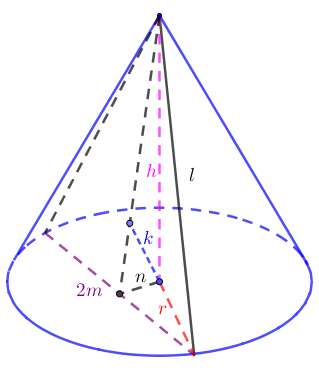
Để làm tốt dạng toán này các bạn cần nắm chắc mối liên hệ giữa các đại lượng: Chiều cao nón (h); Bán kính đáy nón (r); Độ dài đường sinh nón (l); Độ dài dây của đáy (2m); Khoảng cách từ tâm của đáy đến dây (n); Khoảng cách từ tâm của đáy đến thiết diện (k). Xem hình minh họa.
Và sau đây là bảng công thức liên hệ giữa chúng. Hãy lưu lại và học dần nhé.
Nhìn thì cồng kềnh và nhiều như vậy nhưng các bạn cũng chỉ cần sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông là suy ra được.
Về tính chất của thiết diện các bạn cũng có thể dễ dàng thấy đây là một tam giác cân. Vì vậy hãy để ý trong một số bài toán người ta cho vào tam giác này một góc 60 độ thì hãy suy ngay ra nó là tam giác đều nhé.
Ví dụ 1: Cho khối nón có bán kính đáy bằng 3 và chiều cao bằng 4. Mặt phẳng (P) đi qua đỉnh của khối nón cắt đường tròn đáy theo dây cung có độ dài bằng 2. Tính khoảng cách từ tâm của đường tròn đáy đến mặt phẳng (P).
Lời giải:
Ví dụ 2: Cho hình nón có đỉnh S và đáy là đường tròn tâm O bán kính bằng 3. Một mặt phẳng đi qua đỉnh S tạo với đáy của hinh nón một góc 60 độ cắt đướng tròn đáy tại hai điểm A và B. Biết SO=3. Tính diện tích tam giác SAB.
Lời giải:
Trên đây là một số dạng toán liên quan đến hình nón và khối nón thường gặp. Chúc các bạn học tập tốt và đạt kết quả cao. Cảm ơn các bạn đã ghé qua blog. Mời các bạn đọc bài viết tiếp theo về thiết diện qua trục của hình trụ.
Bộ đề thi Online các dạng có giải chi tiết: Mặt Nón – Mặt Trụ – Mặt Cầu
Mặt Nón, Mặt Trụ, Mặt Cầu -