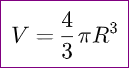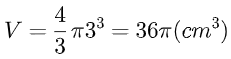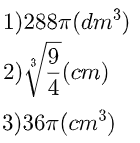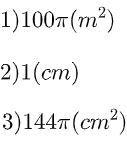Thể tích hình cầu và diện tích mặt cầu
Thể tích hình cầu và diện tích hình cầu được tính như thế nào? Nhìn chung thì 2 công thức về thể tích và diện tích khối cầu cũng khá dễ nhớ. Bài viết dưới đây tôi sẽ giới thiệu đến các bạn 2 công thức đó. Hãy cùng theo dõi nhé!
I. THỂ TÍCH HÌNH CẦU
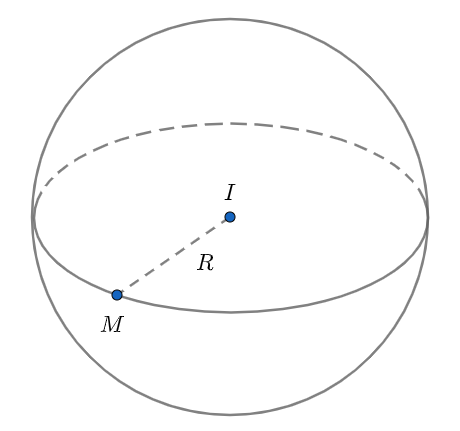
Cho hình cầu (S) có tâm I và bán kính R. Thể tích khối cầu (S) được tính theo công thức sau:
Ví dụ:
Trong không gian cho khối cầu (S) có bán kính bằng 3 cm. Tính thể tích của (S).
Lời giải:
Áp dụng công thức tính thể tích khối cầu ta có thể tích cần tìm là
Một số bài tập tự luyện:
Bài 1. Trong không gian cho khối cầu (S) có bán kính bằng 6 dm. Tính thể tích của (S).
Bài 2. Trong không gian cho khối cầu (S) có thể tích bằng 3π cm³. Tính bán kính của (S).
Bài 3. Trong không gian cho khối cầu (S). Một mặt phẳng đi qua tâm khối cầu và cắt khối cầu theo một hình tròn có diện tích bằng 9π cm². Tính thể tích của (S).
Đáp số tham khảo:
Bộ đề thi Online các dạng có giải chi tiết: Mặt Nón – Mặt Trụ – Mặt Cầu
II. CÔNG THỨC TÍNH DIỆN TÍCH MẶT CẦU
Cho hình cầu (S) có tâm I và bán kính R. Công thức diện tích mặt cầu (S) là
Ví dụ:
Trong không gian cho mặt cầu (S) có tâm I và bán kính bằng 2 cm. Tính diện tích mặt cầu (S).
Lời giải:
Áp dụng công thức tính diện tích hình cầu ta có diện tích cần tìm là
Một số bài tập tự luyện:
Bài 1. Trong không gian cho mặt cầu (S) có tâm I và bán kính bằng 5 m. Tính diện tích mặt cầu (S).
Bài 2. Trong không gian cho mặt cầu (S) có diện tích bằng 4π cm². Tính bán kính mặt cầu (S).
Bài 3. Trong không gian cho mặt cầu (S) có tâm I và đường kính bằng 12 cm. Tính diện tích mặt cầu (S).
Đáp số tham khảo:
Trên đây là 2 công thức tính thể tích khối cầu và tính diện tích mặt cầu. Các bạn hãy luyện tập thật nhiều để vận dụng linh hoạt nhé. Chúc các bạn thành công!
Bộ đề thi Online các dạng có giải chi tiết: Mặt Nón – Mặt Trụ – Mặt Cầu
Mặt Nón, Mặt Trụ, Mặt Cầu -