Tiệm cận của đồ thị hàm số lớp 12

Tiệm cận là gì? Đường tιệm cận của đồ thị hàm số là gì và cách tìm như thế nào? Bài viết dưới đây sẽ giới thiệu tổng quan về đường tιệm.cận của đồ thị hàm số.

Content

1 ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
2 CÁCH TÌM ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
3 MỘT SỐ DẠNG TOÁN THƯỜNG GẶP TRONG THI TRẮC NGHIỆM

ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ

Đường tiệm cận của đồ thị hàm số. Ta có thể hiểu đó là một đường thẳng mà ngày càng đi sát với đồ thị hàm số mà không gặp (không trùng với) đồ thị hàm số. Điều đó không có nghĩa là đường tιệm cận của đồ thị hàm số không cắt đồ thị hàm số. Vì yêu cầu không quá chuyên sâu về vấn đề này mà SGK Giải tích 12 không đề cập một định nghĩa chính xác về đường tιệm cận nói chung mà đưa ra hai định nghĩa về đường tιệm cận đứng và đường tiệm cận ngang của đồ thị hàm số thông qua các giới hạn. Điều có cũng đã gây nên một số tranh cãi như đường thẳng y=1 có là đường tιệm cận ngang của đồ thị hàm số y=1?.

CÁCH TÌM ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ

Cách xác định tiệm cận của đồ thị hàm số lớp 12 là thông qua các giới hạn và giới hạn một bên của hàm số đó tại vô cực hoặc tại các điểm kỳ dị của hàm số đó. Trong đó điểm kỳ dị của hàm số là điểm mà tại đó hàm số không xác định và đồng thời điểm đó phải “dính” với tập xác định của hàm số. Chẳng hạn hàm số y=lnx có tập xác định là (0;+∞) thì 0 là điểm kỳ dị, còn -1 không phải điểm kỳ dị.

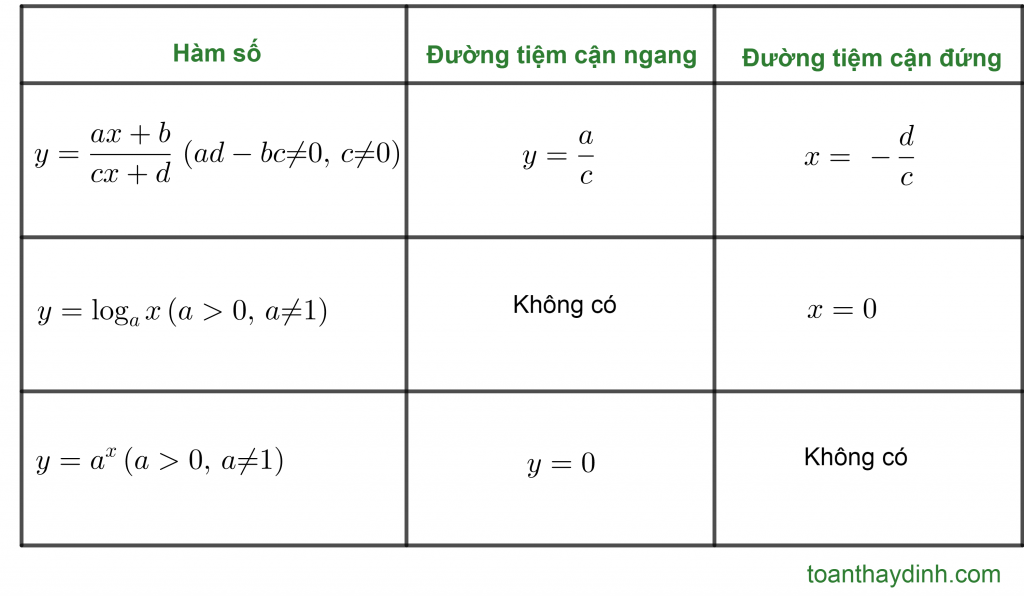
Với mỗi loại hàm số thì có công thức tính tiệm cận khác nhau. Trong chương trình lớp 12 cơ bản chúng ta chỉ cần quan tâm đến tιệm cận của đồ thị hàm số phân thức bậc 1 trên bậc 1 và hàm số mũ, logarit. Và từ đó ta có cách tìm tiệm cận nhanh theo bảng sau:

MỘT SỐ DẠNG TOÁN THƯỜNG GẶP TRONG THI TRẮC NGHIỆM

Trong trắc nghiệm các câu hỏi về đường tιệm cận của đồ thị hàm số đa dạng hơn. Các dạng toán chúng ta thường gặp như:

»» Tìm số tiệm cận của đồ thị hàm số (số đường tiệm cận của đồ thị hàm số). Tìm số đường tiệm cận của đồ thị hàm số là dạng toán phổ biến trong các đề thi trắc nghiệm lớp 12. Cần nhớ rằng đồ thị hàm số có không quá 2 đường tιệm cận ngang. Số tiệm cận của đồ thị hàm số bằng tổng số tιệm cận ngang và số tιệm cận đứng của đồ thị hàm số đó.

Cách tìm số đường tiệm cận của đồ thị hàm số bắt buộc cần tìm tập xác định. Nếu không sẽ dẫn đến các nhầm lẫn. Sai lầm phổ biến là tìm đường tιệm cận ngang nhưng tập xác định lại không chứa vô cực. Chẳng hạn như hàm số y=sqrt(4-x²) không có tιệm cận ngang vì tập xác định của hàm số là [-2;2]. Do đó ta không thể lấy giới hạn của hàm số tại vô cực. Nhưng nếu không tìm tập xác định ta có thể mất thời gian loay hoay tính giới hạn hoặc có thể nhầm lẫn.