Mặt phẳng đối xứng của các khối hình thường gặp
Bài viết dưới đây liệt kê các mặt phẳng đối xứng của các khối đa diện thường gặp như: Khối tứ diện đều, khối lập phương, khối bát diện đều, khối hộp chữ nhật…
Content
- 1 I. MẶT PHẲNG ĐỐI XỨNG LÀ GÌ
- 2 II. SỐ MẶT PHẲNG ĐỐI XỨNG CỦA KHỐI TỨ DIỆN ĐỀU
- 3 III. SỐ MẶT PHẲNG ĐỐI XỨNG CỦA HÌNH LẬP PHƯƠNG
- 4 IV. SỐ MẶT ĐỐI XỨNG CỦA HÌNH HỘP CHỮ NHẬT 3 CHIỀU KHÁC NHAU
- 5 V. SỐ MẶT ĐỐI XỨNG CỦA HÌNH BÁT DIỆN ĐỀU
- 6 VI. SỐ MẶT ĐỐI XỨNG CỦA HÌNH LĂNG TRỤ ĐỨNG TAM GIÁC
- 7 VII. SỐ MẶT ĐỐI XỨNG CỦA HÌNH CHÓP TỨ GIÁC ĐỀU
I. MẶT PHẲNG ĐỐI XỨNG LÀ GÌ
Cho khối đa diện (H). Nếu phép đốι xứng qua mặt phẳng (P) biến (H) thành chính nó. Thì (P) gọi là mặt đốι xứng của khối đa diện (H).
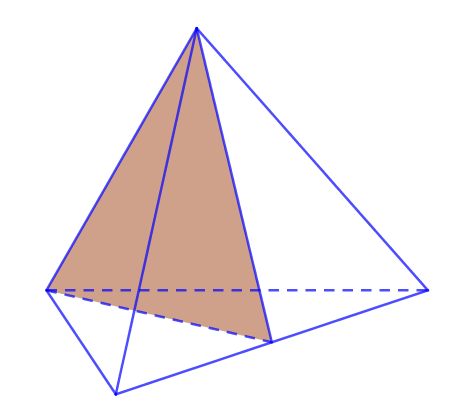
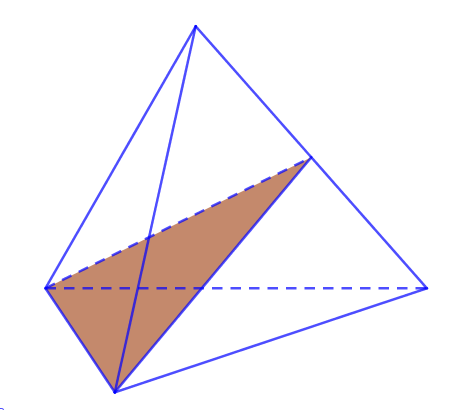
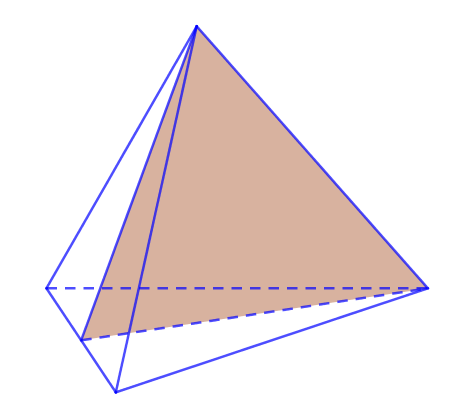
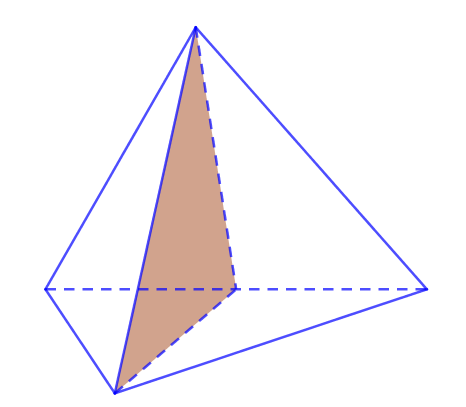
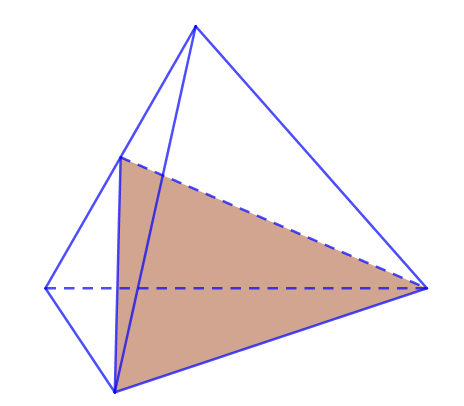
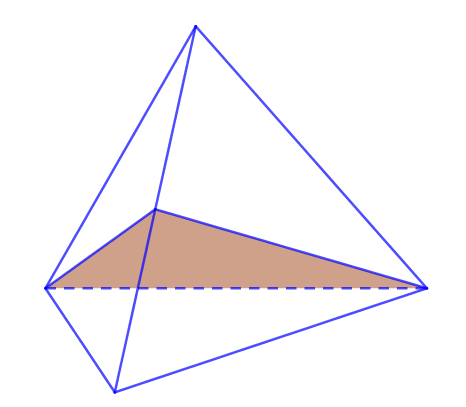
II. SỐ MẶT PHẲNG ĐỐI XỨNG CỦA KHỐI TỨ DIỆN ĐỀU
Có 6 mặt đối xứng của tứ diện đều. Mỗi mặt phẳng đều chứa 1 cạnh và trung điểm cạnh đối diện.
III. SỐ MẶT PHẲNG ĐỐI XỨNG CỦA HÌNH LẬP PHƯƠNG
Có 9 mặt đối xứng của khối lập phương.
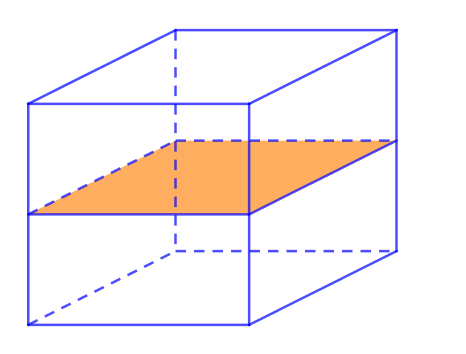
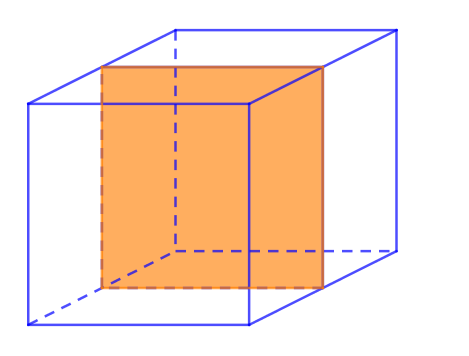
Trong đó có 3 mặt phẳng đi qua trung điểm 4 cạnh song song với nhau chia khối lập phương thành 2 khối hộp chữ nhật.
- (1)
- (2)
- (3)
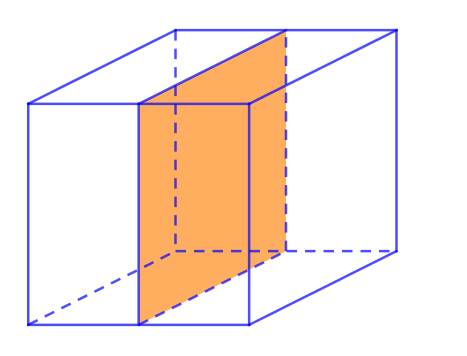
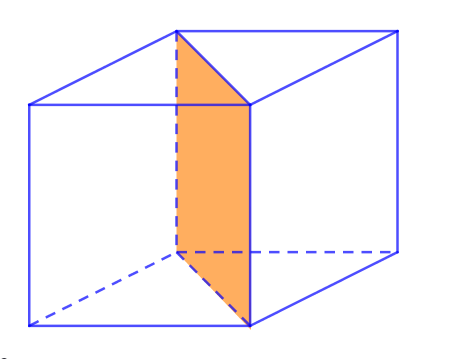
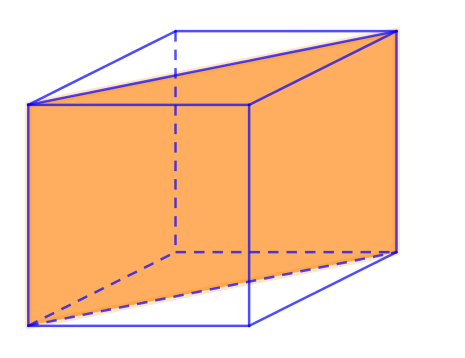
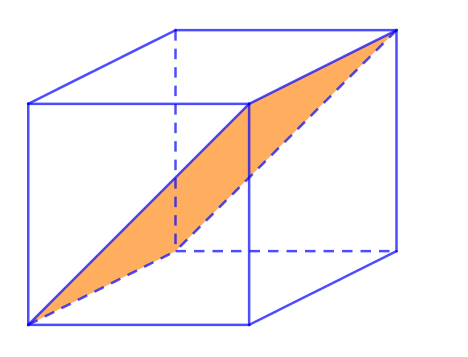
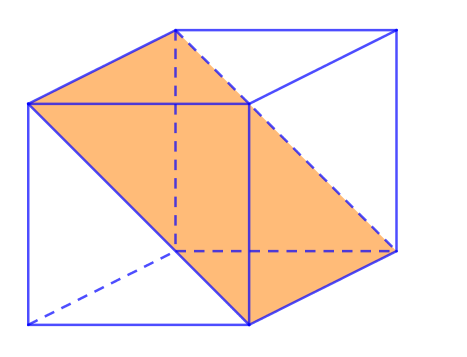
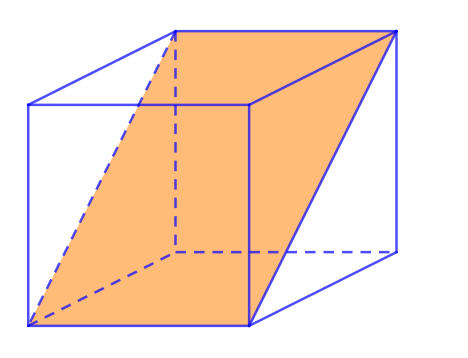
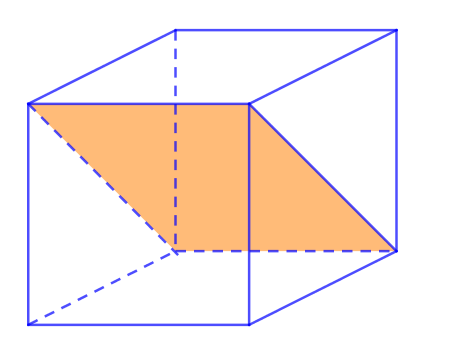
Sáu mặt còn lại chia khối lập phương thành 2 khối lăng trụ tam giác bằng nhau.
- (4)
- (5)
- (6)
- (7)
- (8)
- (9)
IV. SỐ MẶT ĐỐI XỨNG CỦA HÌNH HỘP CHỮ NHẬT 3 CHIỀU KHÁC NHAU
Hình hộp chữ nhật có 3 chiều khác nhau thì chỉ có 3 mặt đối xứng. Và giống 3 trường hợp đầu (1), (2) và (3) của hình lập phương ở trên. Tức là 3 mặt đó, mỗi mặt chia khối hộp chữ nhật thành 2 khối hộp chữ nhật bằng nhau.
Trong trường hợp khối hộp chữ nhật có 2 chiều bằng nhau và 1 chiều khác với 2 chiều đó. Thì ta có thêm 2 mặt đối xứng. Tổng là 5 mặt đối xứng. Chẳng hạn có chiều dài và chiều rộng bằng nhau, chiều cao khác chiều dài và chiều rộng. Thì ta có thêm 2 mặt giống mặt (4) và (5) ở trên.
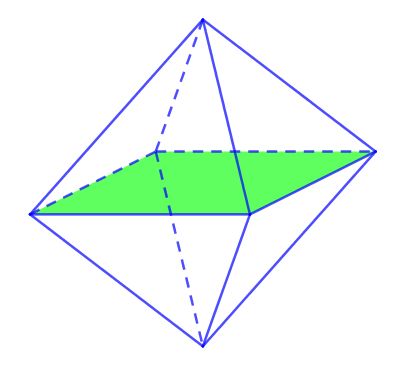
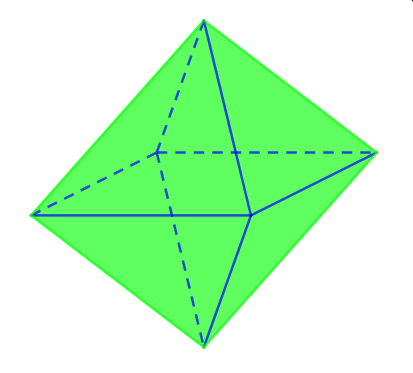
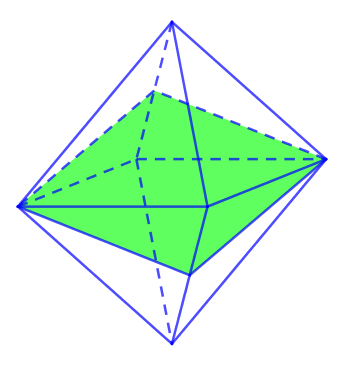
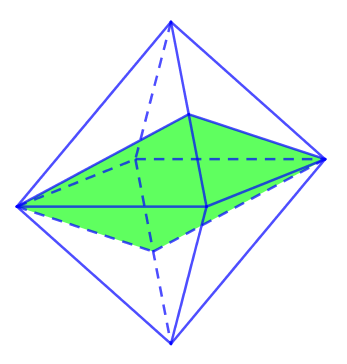
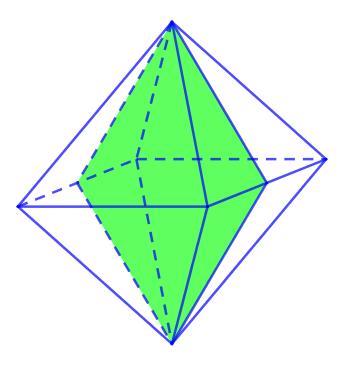
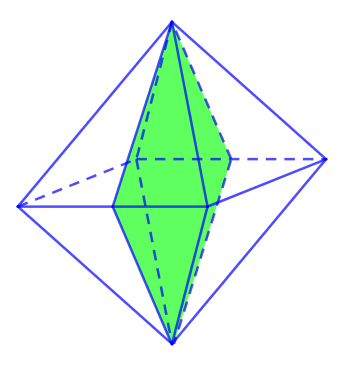
V. SỐ MẶT ĐỐI XỨNG CỦA HÌNH BÁT DIỆN ĐỀU
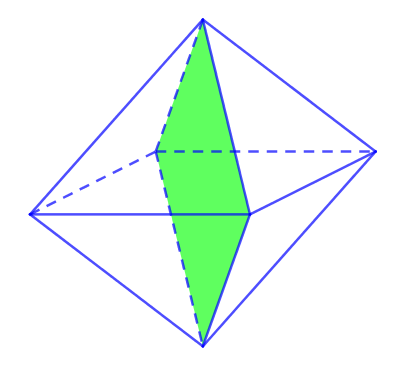
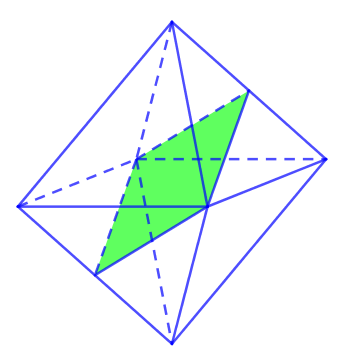
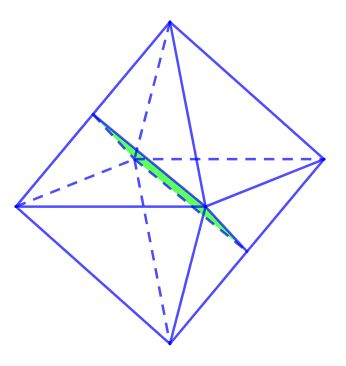
Bát diện đều có tất cả 9 mặt đối xứng.
Trong đó có 3 mặt chia bát diện đều thành 2 khối chóp tứ giác đều mà có tất cả các cạnh bằng nhau.
Còn 6 mặt đối xứng còn lại của bát diện đều đi qua 1 cặp đỉnh đối diện. Mỗi cặp đỉnh có 2 mặt.
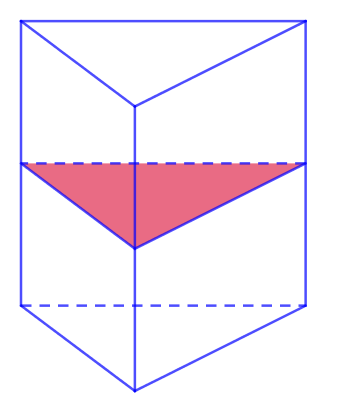
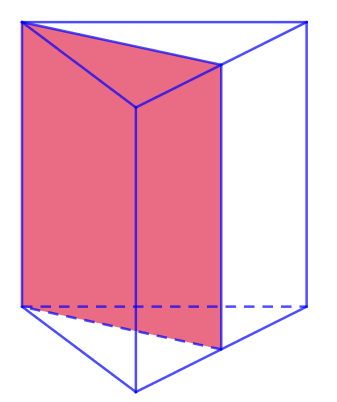
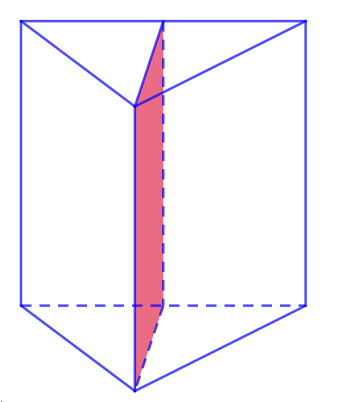
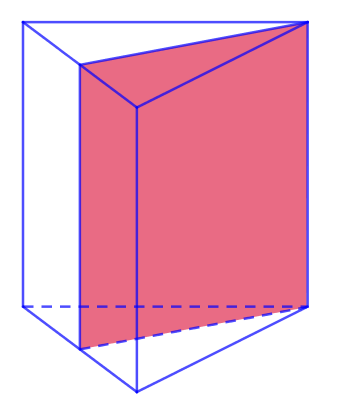
VI. SỐ MẶT ĐỐI XỨNG CỦA HÌNH LĂNG TRỤ ĐỨNG TAM GIÁC
Số mặt đối xứng của lăng trụ đứng tam giác bằng số trục đối xứng của đáy+1.
Chẳng hạn lăng trụ tam giác đều sẽ có 3+1=4 mặt đối xứng.
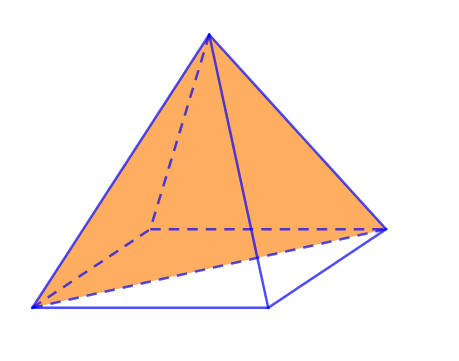
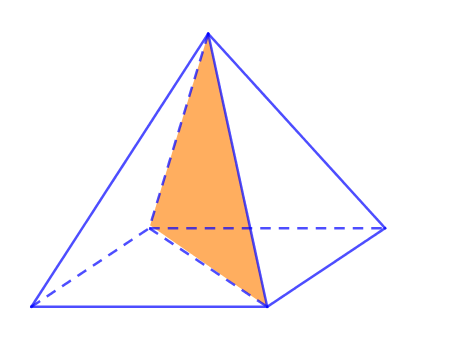
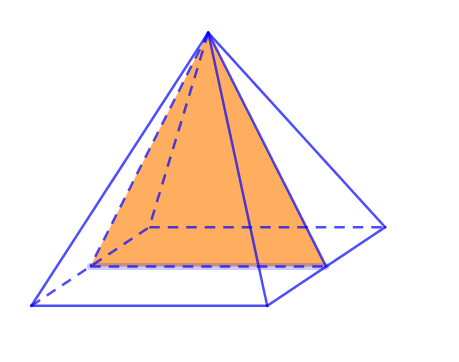
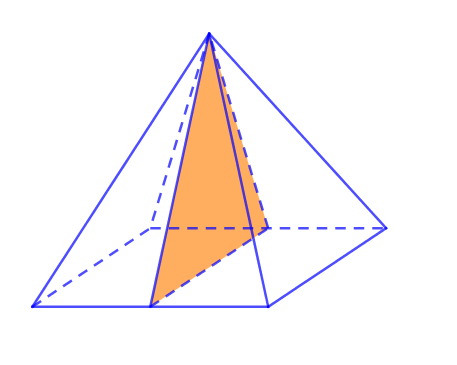
VII. SỐ MẶT ĐỐI XỨNG CỦA HÌNH CHÓP TỨ GIÁC ĐỀU
Khối chóp tứ giác đều có 4 mặt đối xứng.
Trên đây toanthaydinh.com đã liệt kê cho các bạn 1 số hình có các mặt đối xứng như khối tứ diện đều, khối lập phương… để các bạn tiện tra cứu. Chúc các bạn học giỏi!
Xem thêm:
Thể tích tứ diện đều: Khái niệm, công thức và bài tập chi tiết
Khối Đa Diện -