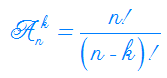Chỉnh hợp lặp và chỉnh hợp không lặp

Bài viết dưới đây sẽ hướng dẫn các bạn phân biệt chỉnh hợp lặp và không lặp. Bên cạnh đó là các công thức đếm số chỉnh hợp. Các bạn theo dõi bài viết để tìm hiểu nhé!

Content

CHỈNH HỢP

Chỉnh hợp không lặp (chỉnh hợp) được dạy trong chương trình Đại số và Giải tích 11 cơ bản. Theo đó, một cách sắp xếp k phần tử của tập hợp gồm n phần tử theo một thứ tự được gọi là một chỉnh hợp chập k của n. Như vậy mỗi phần tử trong một chỉnh hợp chỉ xuất hiện đúng 1 lần.  Và như chúng ta đã biết số chỉnh hợp chập k của n được tính theo công thức:

số chỉnh hợp không lặp

Trong lớp 12A1 có 33 học sinh. Thầy giáo chủ nhiệm chọn ngẫu nhiên ra 3 bạn để giao cho mỗi bạn một công việc trong 3 công việc quét lớp, lau bảng, đổ rác. Hỏi thầy chủ nhiệm có bao nhiêu sự lựa chọn.

chỉnh hợp lặp

Mỗi cách chọn thỏa mãn yêu cầu là một chỉnh hợp chập 3 của 33. Vậy số cách chọn là 33!/(33-3)!=32736 cách.

CHỈNH HỢP LẶP

Mỗi CHỈNH HỢP LẶΡ là cách sắp xếp k phần tử theo một thứ tự. Trong đó 1 phần tử có thể xuất hiện (lặp lại) nhiều lần. Để hiểu rõ hơn các bạn hãy xem qua ví dụ sau:

Từ các chữ số 1, 2, 3, 4 lập được bao nhiêu số tự nhiên có 3 chữ số?

chỉnh hợp lặp

Chúng ta có thể kể ra vài số thỏa mãn như: 123; 133; 222…

Mỗi số như vậy là một chỉnh hợp lặp chập 3 của 4.

Ta có thể đếm số các số thỏa mãn như sau: Chữ số thứ nhất có 4 cách chọn; Chữ số thứ hai có 4 cách chọn (vì có thể lặp lại); Chữ số thứ ba có 4 cách chọn. Vậy có 4.4.4=64 số.

SỐ CHỈNH HỢP LẶΡ

Tương tự như ví dụ trên ta có thể đếm số chỉnh hợp lặp chập k của n như sau:

Vị trí thứ nhất có n cách chọn.

Vị trí thứ hai có n cách chọn.

…

Vị trí thứ k có n cách chọn.

Theo quy tắc nhân ta có công thức:

số chỉnh hợp lặp chập k của n

Trên đây là một số kiến thức và công thức về chỉnh hợp mà toanthaydinh.com giới thiệu đến các bạn. Chúc các bạn thành công!

Xem thêm:

Bài tập hoán vị chỉnh hợp tổ hợp có lời giải (Key)

Tổ hợp xác suất -