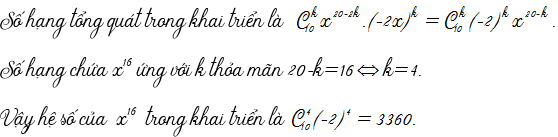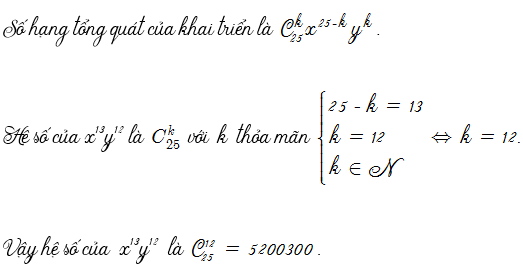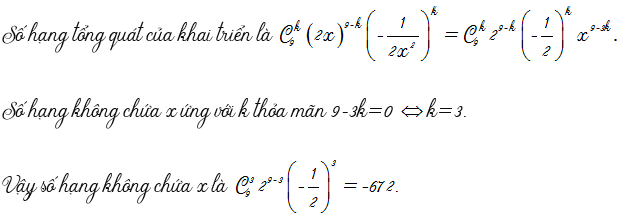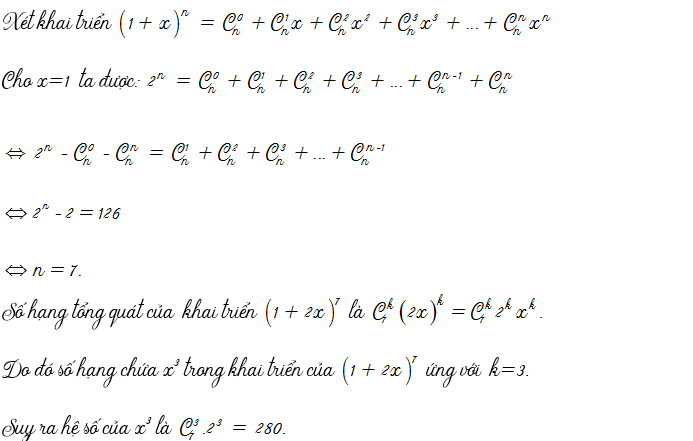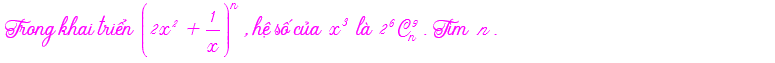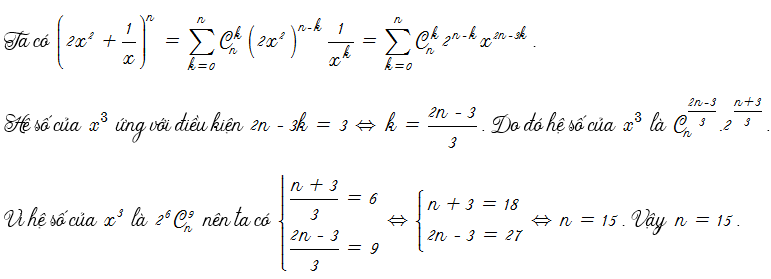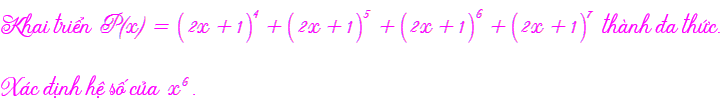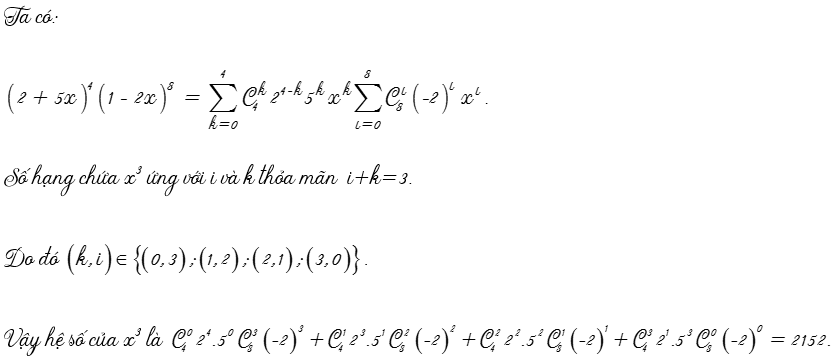Bài tập nhị thức Niu tơn (Newton) tìm số hạng

Bài tập nhị thức Niu tơn là một phần bài tập toán ở lớp 11. Phần lý thuyết và sơ lược vài dạng toán đã được viết trên web này rồi. Các bạn có thể tham khảo thêm tại đây. Bài viết dưới đây tôi sẽ hướng dẫn các bạn cách giải các dạng bài tập về nhị thức Newton tìm hệ số hoặc số hạng. Tập trung vào các dạng cơ bản và kèm theo bài tập. Các bạn cùng theo dõi bài viết để luyện tập luôn nhé!

Content

CÔNG THỨC LŨY THỪA

Hầu hết các bạn khi học đến phần nhị thức Newton đều quên các công thức lũy thừa. Vì vậy trước khi vào giải bài tập nhị thức Newton các bạn cần ôn lại các công thức về lũy thừa. Việc này để hỗ trợ các bạn phần biến đổi số hạng tổng quát trong khai triển nhị thức Newton.

công thức lũy thừa lớp 6

 

BÀI TẬP NHỊ THỨC NIU TƠN TÌM HỆ SỐ HOẶC SỐ HẠNG

Các bạn sẽ gặp các câu hỏi kiểu: “Tìm hệ số của x mũ …trong khai triển của…” ; “Tìm hệ số không chứa x trong khai triển của…”; “Tìm số hạng chứa x mũ …trong khai triển của…” hoặc các câu hỏi kiểu tương tự.

Vậy bài này giải thế nào cho nhanh? Thực ra có rất nhiều kiểu trình bày nhưng chung bản chất. Theo quan điểm cá nhân của tôi thì các bạn cứ dùng số hạng tổng quát (số hạng thứ k+1) sau đó cô lập 2 phần hệ số và ẩn. Tiếp theo tùy vào yêu cầu bài toán, các bạn cho số mũ của ẩn bằng số mũ cần tìm. Từ đó các bạn tìm được chỉ số. Cuối cùng thay chỉ số ngược lại phần hệ số hoặc thay vào số hạng tùy theo yêu cầu bài toán.

bài tập nhị thức niu tơn lớp 11

Nếu khai triển có nhiều hơn 1 ẩn thì cách làm hoàn toàn tương tự. Chỉ khác ở đây là chúng ta cần 1 hệ điều kiện để tìm chỉ số.

bài tập về nhị thức niu tơn có lời giải

Với bài toán tìm số hạng không chứa x thì thực chất là tìm hệ số của số hạng chứa xº.

bài tập về nhị thức niu tơn

Trong một số bài toán tìm hệ số hay số hạng trong khai triển của nhị thức Newton. Có đi kèm với yêu cầu tìm n thỏa mãn một phương trình đại số tổ hợp. Chúng ta tìm n bằng cách giải phương trình trước. Sau đó quay trở lại dạng giống các ví dụ bên trên.

bài tập nhị thức niu tơn lớp 11 có đáp án

Hoặc người ta cũng có thể cho hệ số của khai triển chưa biết n và yêu cầu tìm n. Khi đó ta dùng số hạng tổng quát để lập phương trình tìm n.

bài tập nhị thức newton toán thầy định

bài tập nhị thức newton lớp 11 co loi giai

bài tập về nhị thức newton có lời giải

BÀI TẬP TÌM HỆ SỐ HOẶC SỐ HẠNG CỦA TỔNG HOẶC TÍCH NHIỀU NHỊ THỨC NIU TƠN

Nếu trong biểu thức có tổng (hiệu) nhiều nhị thức Newton thì chúng ta cần đánh giá xem nhị thức nào chứa số mũ cần tìm. Việc này giúp chúng ta giảm bớt thời gian khai triển các nhị thức.

tổng của nhiều nhị thức Newton

giải nhanh nhị thức New tơn

Nếu bài toán chứa tích các nhị thức thì phức tạp hơn nhiều. Trong trường hợp này chúng ta cần khai triển các nhị thức với chỉ số chạy độc lập. Sau đó xét tổng các chỉ số để thỏa mãn yêu cầu bài toán. Giải thích bằng lời khá khó hiểu nên các bạn chịu khó theo dõi ví dụ sau nhé.

tích nhiều nhị thức niu tơn

Trên đây là một số dạng toán tìm hệ số của khai triển nhị thức Newton mà toanthaydinh.com giới thiệu đến các bạn. Còn một số dạng toán nữa như tìm hệ số khai triển của tam thức thì vượt ra ngoài chương trình cơ bản của phổ thông. Nên không được đề cập đến ở đây. Chúc các bạn học giỏi và thành công!

Xem thêm:

Tính tổng liên quan đến nhị thức Newton (Niu tơn)

Tổ hợp xác suất -