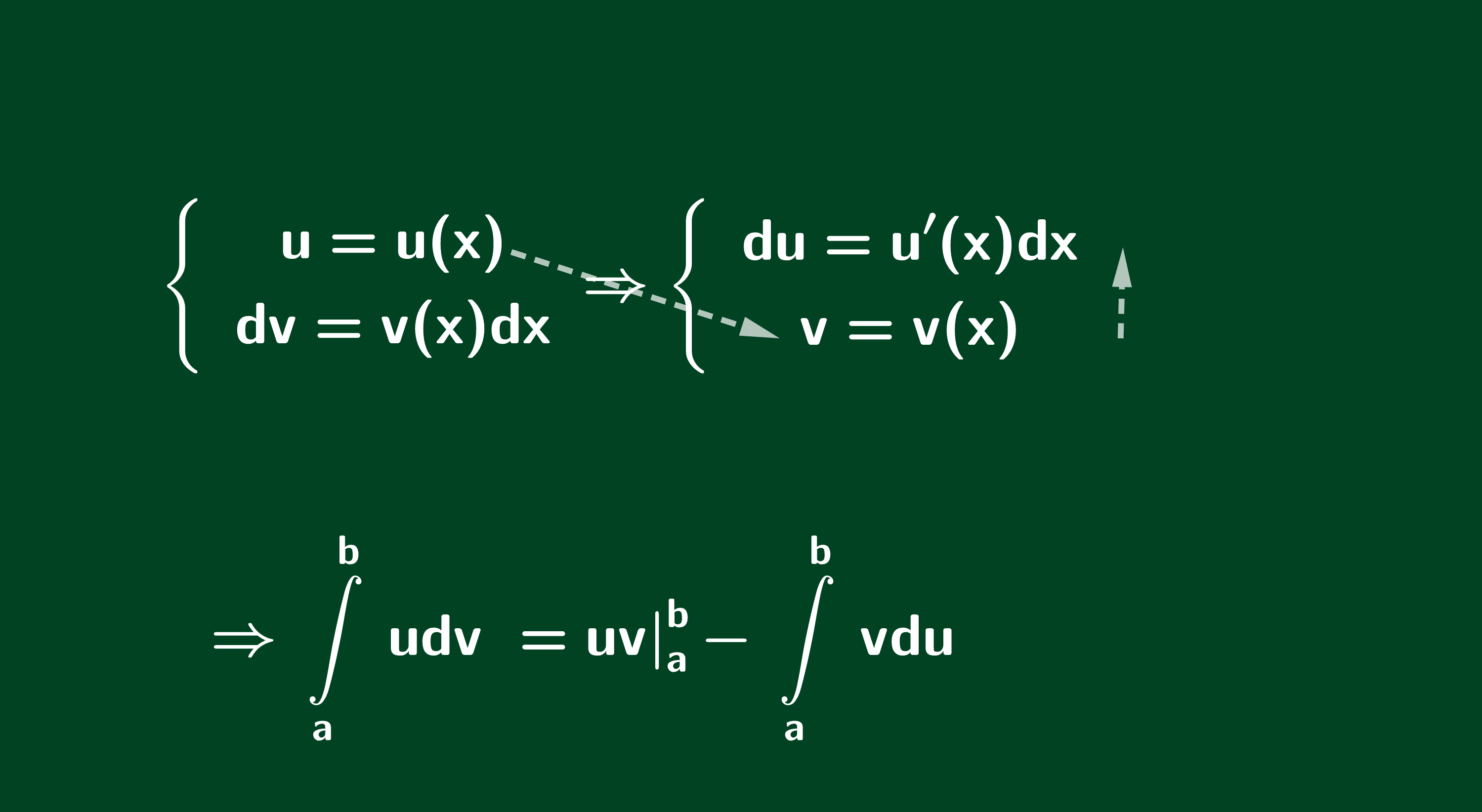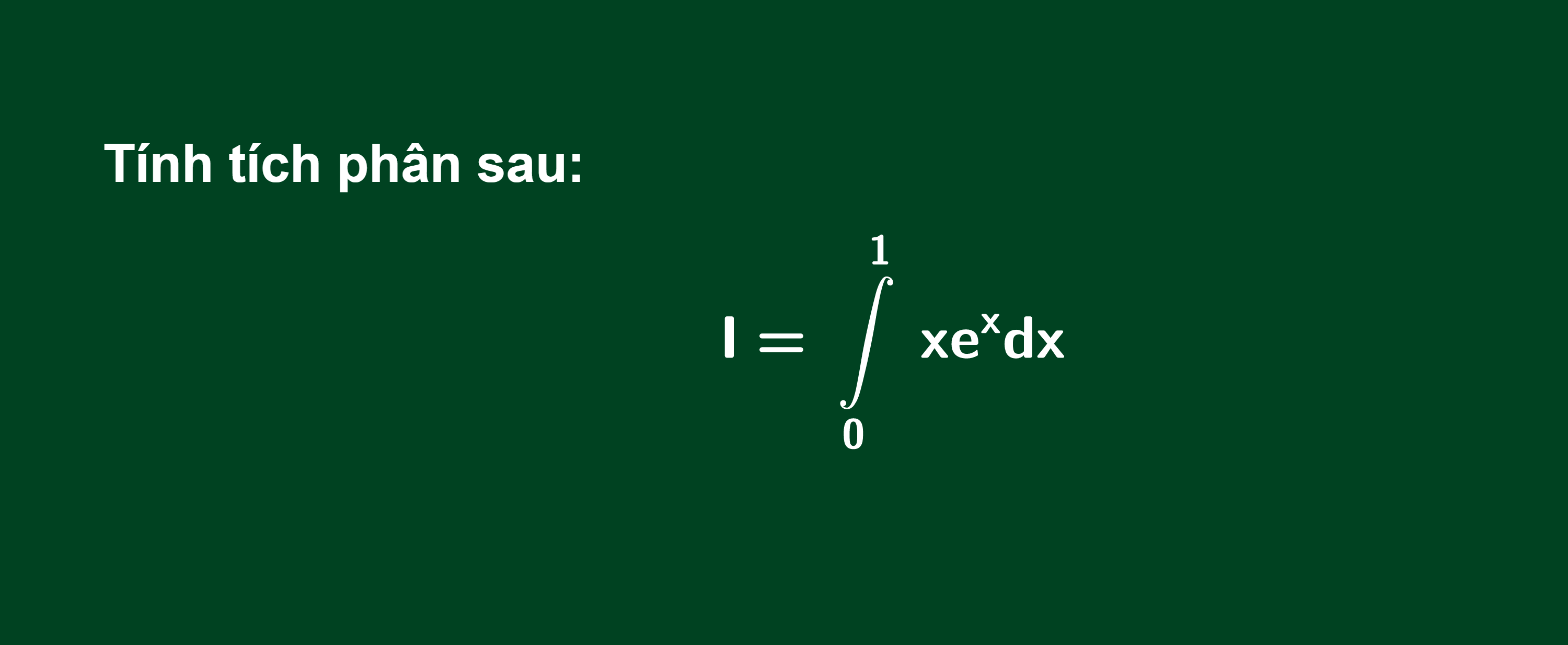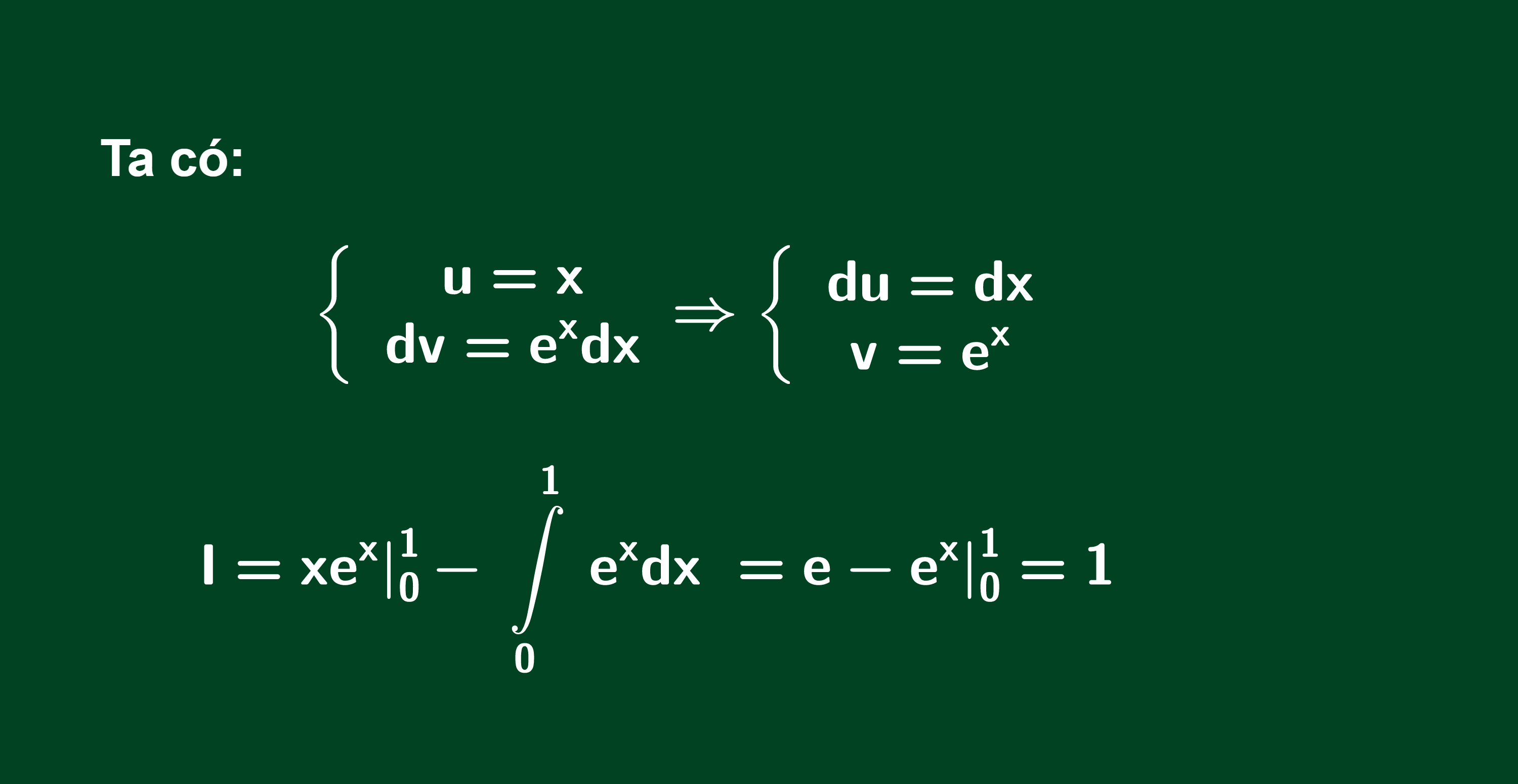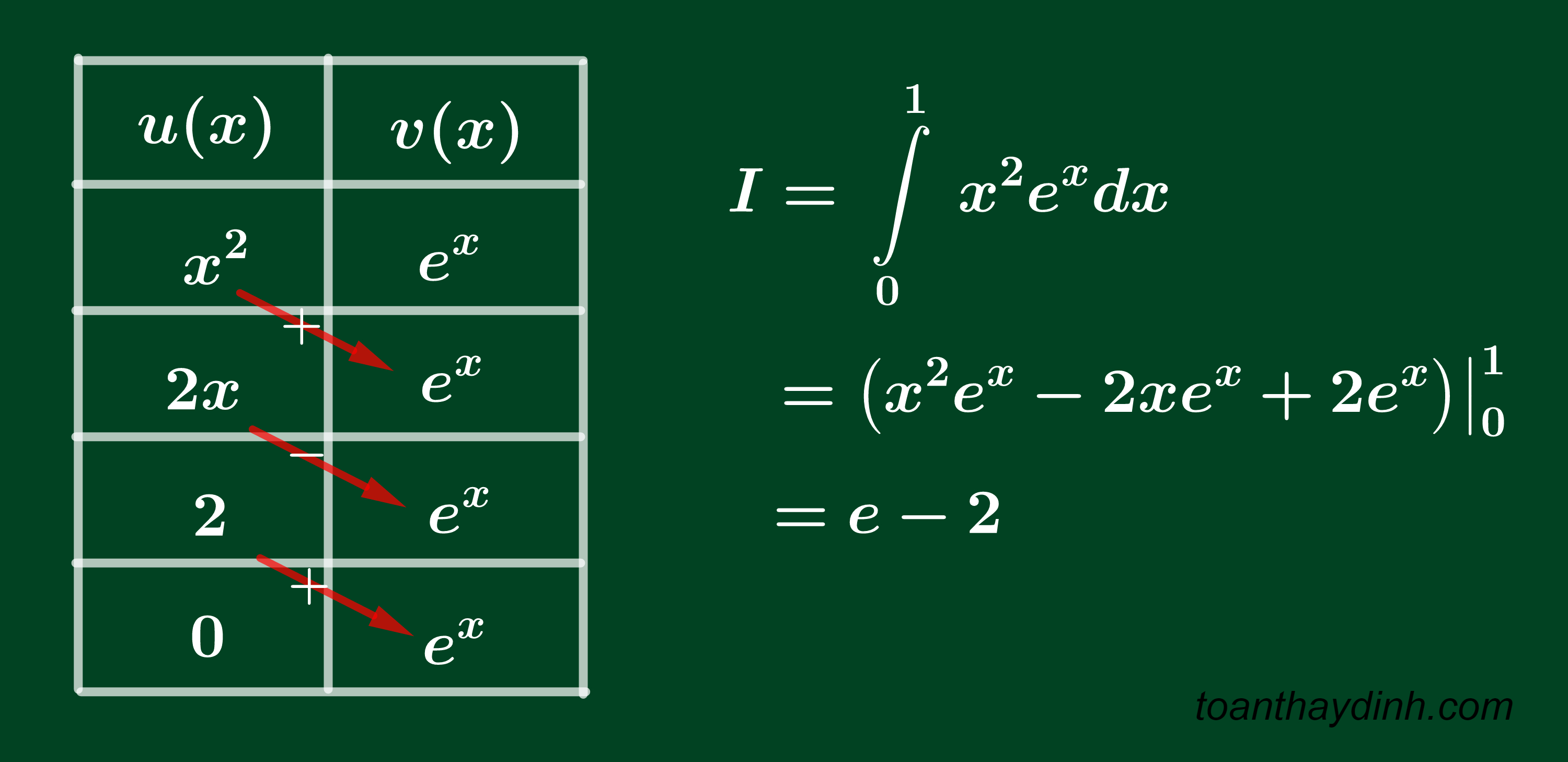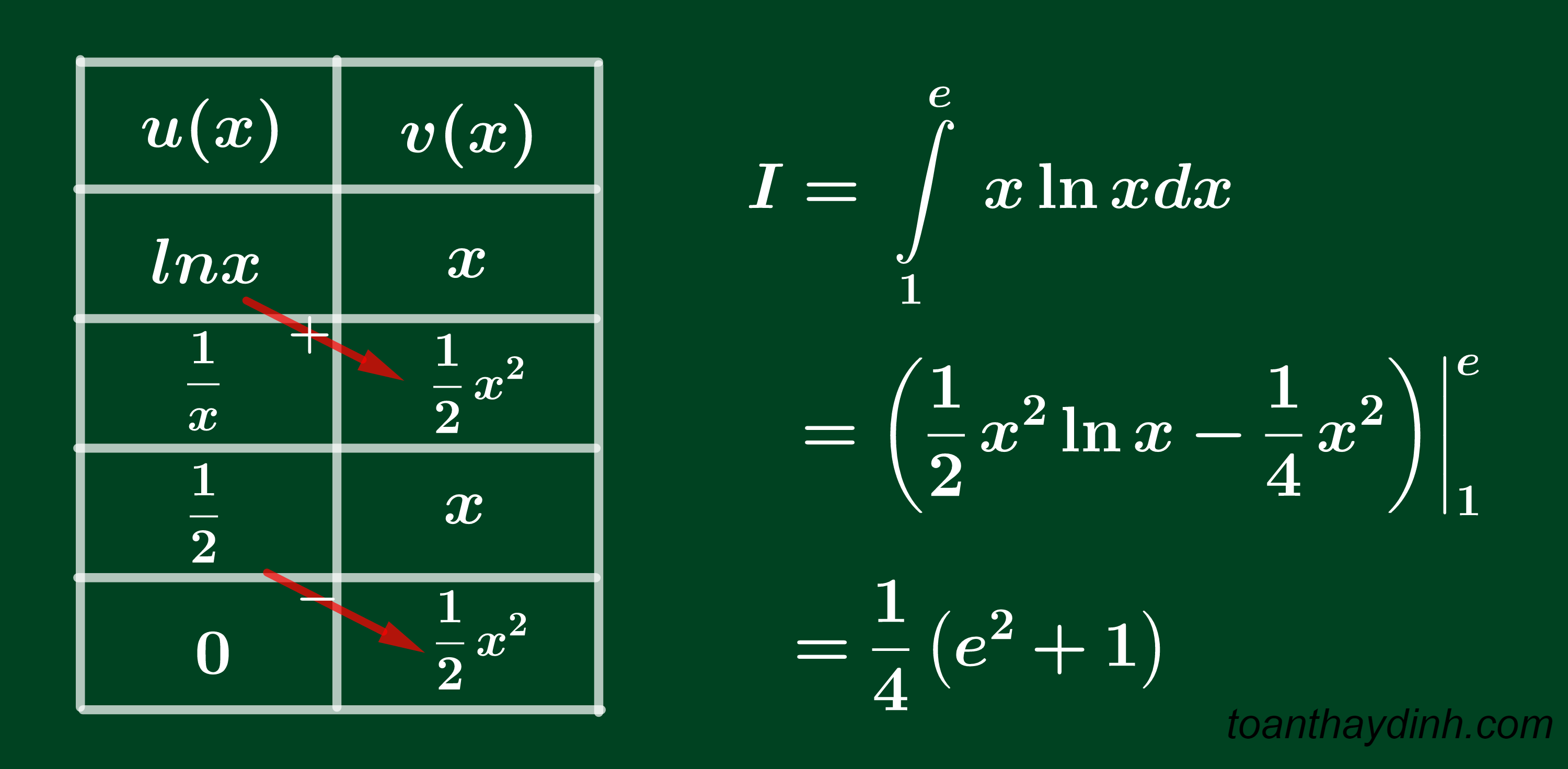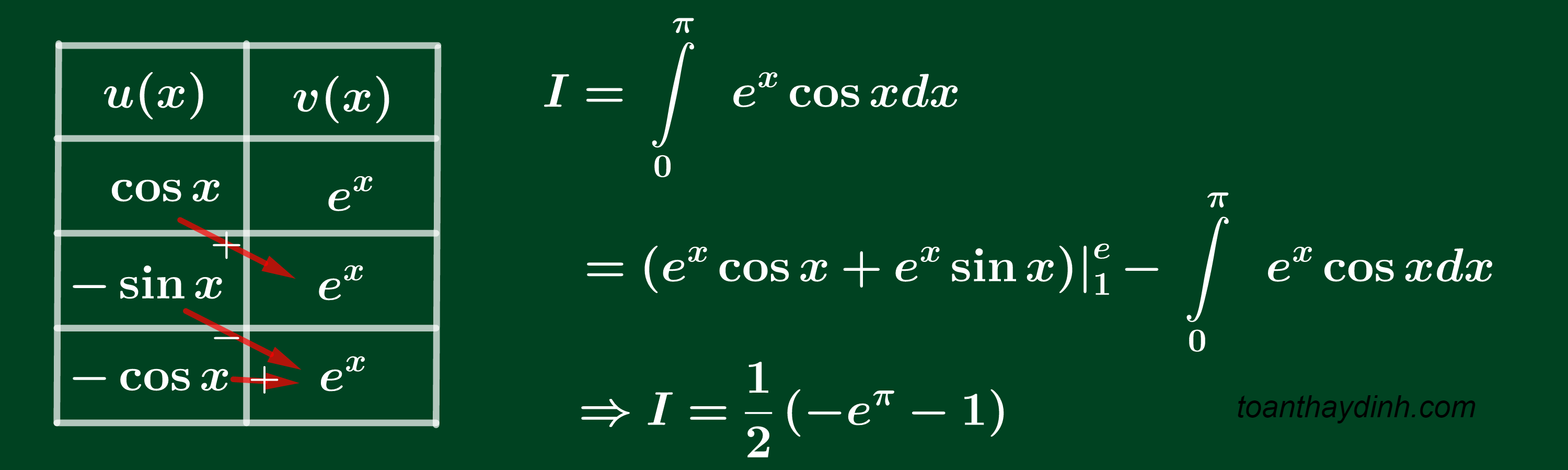Tích phân từng phần tính nhanh bằng sơ đồ

Tích phân từng phần (tptp) và phương pháp đổi biến số là hai trong các phương pháp tính tích phân. TPTP được sử dụng khi biểu thức dưới dấu tích phân chứa 2 loại hàm số khác nhau trong 4 loại hàm số: logarit, đa thức, lượng giác, hàm số mũ. Cũng có khi phương pháp này được dùng trong các bài toán tích phân hàm ẩn.

Content

CÔNG THỨC TÍCH PHÂN TỪNG PHẦN

Với điều kiện các hàm số khả tích trên đoạn [a;b], ta có:

"Công

PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN

Từ công thức trên, ta có sơ đồ như sau:

phương pháp tính tích phân từng phần

Vấn đề tiếp theo là ta chọn u(x) như thế nào. Để giải quyết vấn đề này chúng ta cùng làm theo câu “thần chú” sau nhất lô, nhì đa, tam lượng, tứ mũ. Tức là thứ tự ưu tiên đặt u(x) là lôgarit, đa thức, lượng giác và mũ. Để hiểu rõ hơn chúng ta cùng xét một ví dụ đơn giản sau:

Ví dụ:

tích phân toàn phần

Phân tích: Trong biểu thức dưới dấu tích phân ta thấy có hàm đa thức x và hàm mũ e^x. Do đó theo thứ tự ưu tiên như đã nói ở trên trên ta đặt u(x)=x, những phần còn lại sẽ là dv.

Lời giải:

cách tính tích phân từng phần

Chú ý: Với một số tích phân mà “xử” 1 lần rồi mà vẫn chưa ra được đáp số, ta “xử” tiếp lần thứ hai…

Bài tập Nguyên Hàm Online có giải chi tiết:

Đề thi Online có giải: Đề 1 [7-8 điểm] Tích phân từng phần

Bộ đề thi Online các dạng có giải chi tiết: Nguyên Hàm Tích Phân

TÍNH TÍCH PHÂN TỪNG PHẦN NHANH BẰNG SƠ ĐỒ

Có những tích phân mà ta phải tính tích phân từng phần hai lần trở lên. Chúng ta lập sơ đồ tính nhanh tích phân để cho ra ngay kết quả một cách nhanh chóng. Tuy nhiên tùy từng cặp hàm số dưới dấu tích phân ta lại lập các sơ đồ tính nhanh nguyên hàm từng phần khác nhau.

DẠNG ĐA THỨC−MŨ, ĐA THỨC-LƯỢNG GIÁC

Đối với tích phân dạng này ta lập sơ đồ 2 cột. Cột 1 là u(x) ứng với đa thức và lấy đạo hàm đến khi bằng 0. Cột 2 là v(x) ứng với mũ hoặc lượng giác và lấy nguyên hàm đến khi ngang với cột 1. Sau đó ta lấy nguyên hàm theo quy tắc nhân chéo đan dấu. Để rõ hơn chúng ta cùng xét ví dụ sau:

Ví dụ:

Tính tích phân: I = \int\limits_0^1 {{x^2}{e^x}dx} .

Lời giải:

Theo quy tắc nhất lô, nhì đa, tam lượng, tứ mũ ta đặt u(x)=x², dv=e^xdx. Nếu tính thông thường như trên ta cần lấy 2 lần tích phâ n từng phần. Nếu thực hiện theo sơ đồ dưới đây ta có thể viết ra nguyên hàm ngay. 

Tính nhanh tích phân từng phần

Lưu ý: Trong lời giải trên thì cột bên trái lấy đạo hàm liên tục đến 0. Cột bên phải lấy nguyên hàm đến khi ngang số 0 cột bên trái. Khi lấy tích theo mũi tên màu đỏ thì mũi tên đầu tiên lấy dấu+ sau đó đan dấu.

DẠNG ĐA THỨC-LOGARIT

Tương tự như trên nhưng đối với dạng đa thức – logarit, chúng ta phải đặt u(x) là logarit nên cột 1 không thể đạo hàm đến 0 được. Vì vậy ta phải xử lý bằng cách ở dòng thứ 3 của bảng ta lấy hàng 3 cột 1 nhân hàng 3 cột 2 sau đó tách hệ số thành hàng 4 cột 1 phần ẩn thành hàng 4 cột 2. Lưu ý bỏ nhân chéo hàng 3 và 4 và vẫn đan dấu như dạng trên nhé. Để hiểu rõ hơn chúng ta cùng xét một ví dụ sau.

Ví dụ:

Tính tích phân I = \int\limits_1^e {x\ln xdx} .

Lời giải:

Tích phân từng phần có e

Lưu ý: Ở hàng 3 cột 2 chúng ta nên chọn nguyên hàm sao cho khi nhân vào hàng 3 cột 1 được biểu thức đơn giản nhất có thể.

TÍCH PHÂN LẶP (MŨ−LƯỢNG GIÁC)

Vì nguyên hàm của dạng tích của mũ và lượng giác là dạng nguyên hàm xoay vòng. Tức là dùng nguyên hàm từng phần 2 lần thì xuất hiện biểu thức nguyên hàm có trong đề bài. Nên chúng ta cũng thực hiện tương tự như dạng thứ nhất trong bài viết này đến khi biểu thức lặp lại theo tích hàng ngang.  Ta lấy tích ngang hàng cuối nằm trong dấu tích phân. Sau đó ta chuyển vế và rút gọn để được kết quả.

Ví dụ:

Tính tích phân sau I = \int\limits_0^\pi {{e^x}\cos xdx}

Lời giải:

Tích phân từng phần công thức

Cách tính không hề khó như chúng ta tưởng phải không nào. Hãy nắm chắc “thần chú” và bảng nguyên hàm để xử nhanh dạng toán này nhé.

 

Chúc các em thành công!

Xem thêm:

Ứng dụng tích phân trong hình học

Khái niệm tích phân cơ bản và phương pháp tính tích phân nhanh

Nguyên Hàm - Tích Phân -