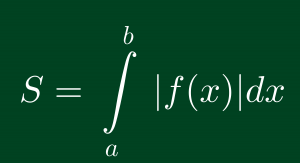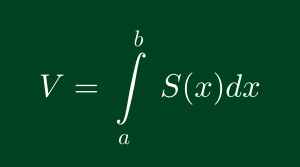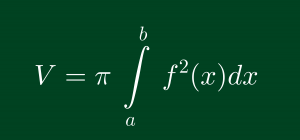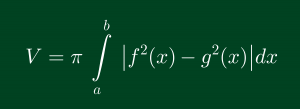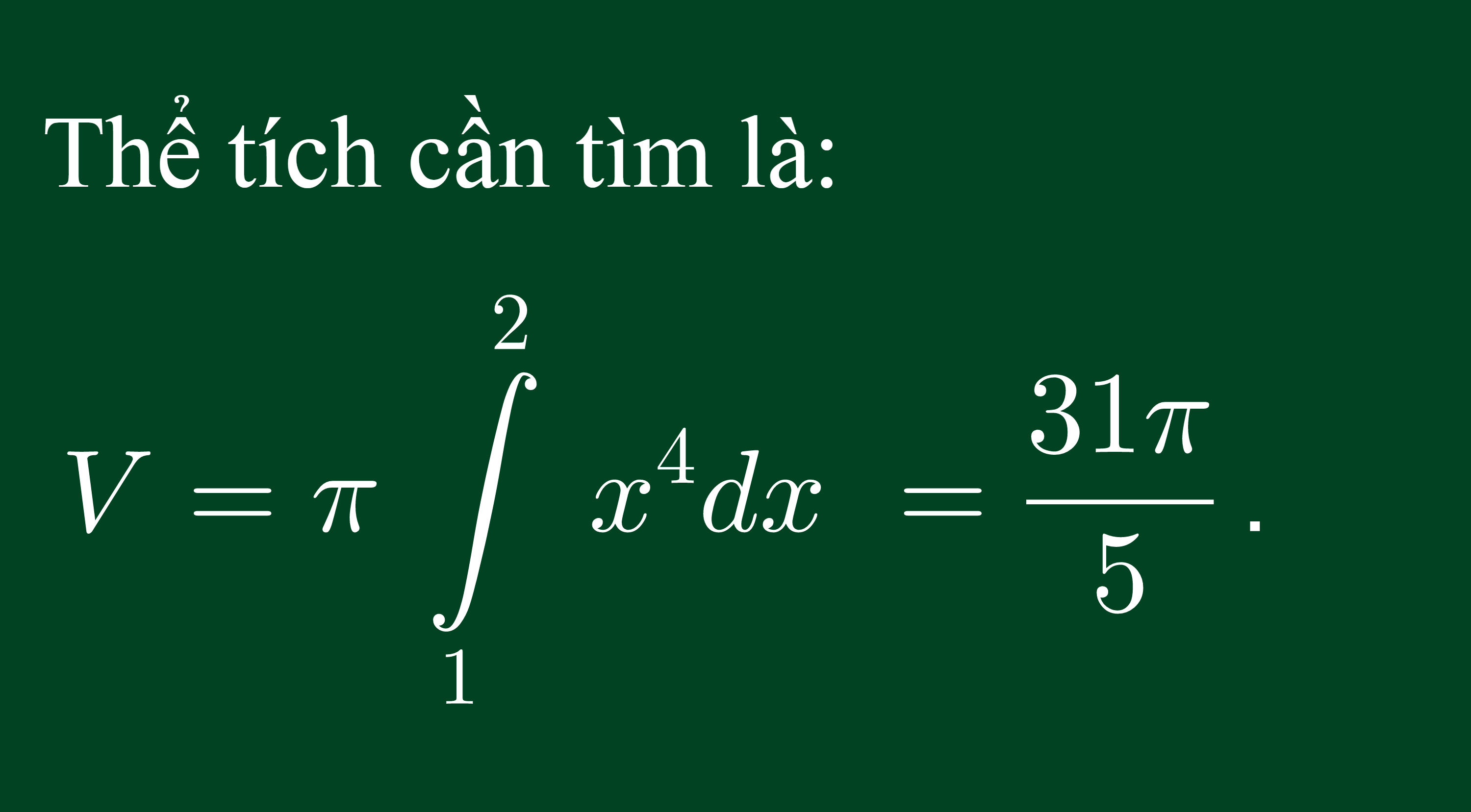Ứng dụng tích phân trong hình học
Ứng dụng tích phân trong hình học bao gồm: Tính diện tích hình phẳng, tính thể tích vật thể.
ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG
Nếu hàm số f(x) và g(x) cùng liên tục trên [a;b] thì diện tích hình phẳng giới hạn bởi các đường y=f(x), y=g(x), x=a, x=b được tính theo công thức sau:
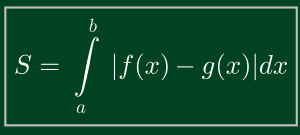
Ứng dụng tích phân tính diện tích
Trong trường hợp đặc biệt đồ thị y=g(x) là trục hoành thì diện tích hình phẳng tính theo công thức
Những bài tính diện tích hình phẳng đã có cận rõ ràng, ta chỉ việc áp dụng công thức trên. Trong trường hợp các cận của tích phân chưa xác định ta xét phương trình hoành độ giao điểm để tìm cận. Nếu như hình phẳng giới hạn bởi hơn hai đường cong ta cần vẽ đồ thị.
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi các đường cong y=x và y=x².
Lời giải:
Phân tích: Hình phẳng giới hạn bởi hai đường cong và chưa có cận, vì vậy ta cần giải phương trình hoành độ giao điểm để tìm cận.
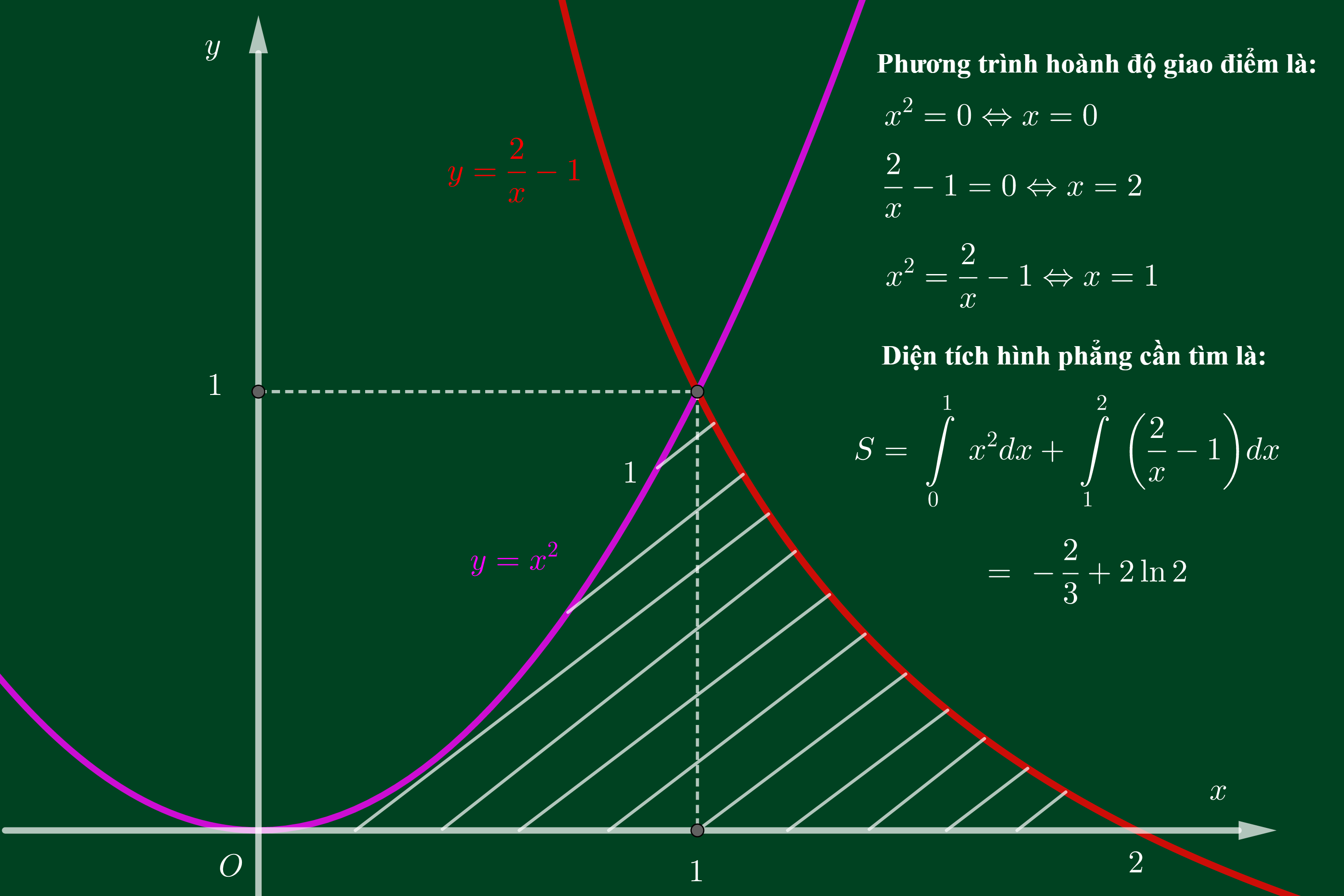
Ví dụ 2: Tính diện tích hình phẳng giới hạn bởi các đường .
Phân tích: Hình phẳng trên giới hạn bởi ba đường cong và chưa có cận. Vì vậy ta cần vẽ hình, giải các phương trình hoành độ giao điểm để xác định cận.
Bài tập Nguyên Hàm Online có giải chi tiết:
Đề thi Online có giải: Đề 1 [5-6 điểm] Ứng dụng tích phân để tìm diện tích
Bộ đề thi Online các dạng có giải chi tiết: Nguyên Hàm Tích Phân
ỨNG DỤNG TÍCH PHÂN TÍNH THỂ TÍCH
Tính thể tích bằng tích phân
Trong không gian Oxyz, vật thể V được giới hạn bời hai mặt phẳng vuông góc với trục Ox là x=a, x=b. Một mặt phẳng tùy ý vuông góc với Ox tại điểm x (a≤x≤b) cắt V theo thiết diện có diện tích S(x). Giả sử S(x) liên tục trên [a;b]. Khi đó thể tích vật thể V được tính theo công thức:
Đặc biệt, đối với vật thể tròn xoay được sinh ra bởi hình phẳng giới hạn bởi các đường x=a, x=b,y= f(x), Ox khi quay quanh trục Ox có thể tích là:
Với vật thể tròn xoay được sinh ra bởi hình phẳng giới hạn bởi các đường x=a, x=b,y= f(x), y=g(x), Ox khi quay quanh trục Ox có thể tích là:
Ví dụ: Cho (H) là hình phẳng giới hạn bởi các đường x=1;x=2, y=x², Ox. Gọi V là vật tròn xoay khi quay (H) quanh trục Ox. Tính thể tích của V.
Lời giải:
Ứng dụng của tích phân trong hình học là một ứng dụng quan trọng. Nó không chỉ quan trọng trong giải bài tập toán. Nó còn giúp chúng ta giải quyết các bài toán thực tế trong cuộc sống chúng ta nữa. Vấn đề này sẽ được đề cập trong một bài viết khác.
Chúc các em thành công!
Xem thêm:
Tích phân hàm ẩn – Lý thuyết và bài tập minh họa
Bộ đề thi Online các dạng có giải chi tiết: Nguyên Hàm Tích Phân
Nguyên Hàm - Tích Phân -