Lý thuyết về tập hợp lớp 10 cơ bản
Xuyên suốt chương trình toán phổ thông là quá trình xây dựng các tập hợp số. Điều này hoàn toàn phù hợp với lịch sử phát triển của loài người từ thuở sơ khai đến nay. Bài viết dưới đây sẽ giới thiệu đến bạn đọc về các tập số cũng như sơ lược lịch sử dẫn đến sự hình thành chúng. Vì bài viết động chạm tới lịch sử hàng ngàn năm của loài người nên chắc chắn không thể chính xác hoàn toàn được.
Content
1. KHÁI NIỆM VÀ CÁCH XÁC ĐỊNH TẬP HỢP
Tập hợp là một khái niệm nguyên thủy của toán học. Nó không có định nghĩa mà chỉ có thể mô tả về nó như là một nhóm các đối tượng. Mà mỗi đối tượng được gọi là một phần tử. Chẳng hạn tập các số tự nhiên lẻ nhỏ hơn 10 có thể được viết là A={1;3;5;7;9}. Các phần tử của A là 1; 3; 5; 7; 9.
Có 2 cách để viết một tập. Một là là liệt kê. Hai là chỉ ra tính chất đặc trưng.
Ví dụ về liệt kê: A={0;1;2;3}.
Ví dụ về chỉ ra tính chất đặc trưng: A={x∈N|x<3}.
Hai tập hợp bằng nhau nếu mọi phần tử của tập này đều là phần tử của tập kia và ngược lại.
2. TẬP HỢP CÁC SỐ TỰ NHIÊN
Số tự nhiên có lịch sử lâu đời nhất của loài người. Các nhà khoa học cho rằng số tự nhiên hình thành từ hàng trăm năm trước công nguyên. Nó được sinh ra từ nhu cầu đếm của con người. Về vấn đề này, ở Việt Nam có lẽ bạn nên đọc cuốn sách ” Chữ số và thế giới” của tác giả Đỗ Minh Triết sẽ có câu trả lời tốt nhất về lịch sử số tự nhiên.
Riêng về vấn đề tập số tự nhiên có số 0 hay không thì chúng ta tuân theo quy ước của từng cuốn sách.
3. TẬP HỢP SỐ NGUYÊN
Một cách rất tự nhiên thì ngoài phép toán cộng (thêm vào) ta cần có phép toán trừ (bớt đi). Dễ thấy rằng với tập số tự nhiên thì phép toán cộng luôn thực hiện được. Nhưng phép toán trừ thì lại không phải lúc nào cũng thực hiện được. Chẳng hạn ta không thể lấy 3 trừ 5 trong tập số tự nhiên. Vì vậy tự nhiên chúng ta sẽ có khái niệm số âm. Tập gồm các số nguyên dương, các số nguyên âm và số 0 là tâm hợp số nguyên.
4. TẬP HỢP SỐ HỮU TỶ
Quá trình phát triển của loài người có những công việc cần đến sự phân chia. Từ việc nhỏ như chia một cái bánh đến việc lớn như chia đất đai. Trên tập số nguyên thì phép chia không phải lúc nào cũng thực hiện được. Như không có số nguyên nào thể hiện kết quả của phép chia 1 cho 3. Từ đó rất tự nhiên khái niệm số hữu tỷ được hình thành.
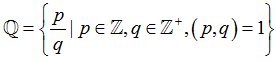
5. TẬP SỐ THỰC
Ta có một cách giải thích khác về tiến trình hình thành các tập số. Đó là trong quá trình giải các phương trình đại số thì phương trình bị vô nghiệm. Việc mở rộng các tập số khiến cho các phương trình đại số có nghiệm. Chẳng hạn, trên tập số tự nhiên thì phương trình x+1=0 vô nghiệm. Nhưng trên tập số nguyên phương trình đó có nghiệm x=-1. Trong đó -1 là một số âm. Trên tập số nguyên thì phương trình 2x+3=0 vô nghiệm. Nhưng 2x+3=0 lại có nghiệm x=-2/3 trên tập số hữu tỷ.
Trên tập số hữu tỷ thì phương trình x²-2=0 không có nghiệm.
Thực vậy:
Tuy nhiên về mặt hình học ta thấy hoàn toàn tồn tại một số như vậy.
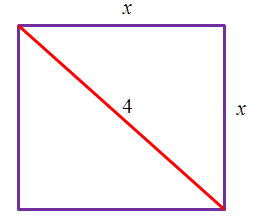
Rõ ràng tồn tại một hình vuông có đường chéo bằng 4. Ta giả sử độ dài cạnh của nó là x. Theo định lý Pytago ta có phương trình x²+x²=4. Hay x²=2. Vậy tồn tại một số mà bình phương của nó bằng 2. Mà số đó lại không phải số hữu tỷ. Người ta gọi đó là số vô tỷ. Việc bổ sung số vô tỷ vào số hữu tỷ đã tạo nên tập số thực.
Trên trục số, bên cạnh một số hữu tỷ luôn có một số vô tỷ và ngược lại. Người ta chứng minh được tập số thực đã lấp đầy trục số.
6. TẬP SỐ PHỨC
Nếu giải thích như đối với cách hình thành số thực thì ta thấy phương trình x²+1=0 không có nghiệm thực. Rõ ràng là như thế. Trên tập số thực là một tập sắp thứ tự thì x² là một số không âm. Do đó x²+1 không thể bằng không được. Chính vì mâu thuẫn đó đã dẫn đến sự hình thành khái niệm số phức. Số phức là số có dạng a+bi với a, b là các số thực và i là đơn vị ảo thỏa mãn i²=-1.
Như vậy bài viết đã giới thiệu sơ lược đến các bạn các tập số có trong chương trình toán phổ thông. Bài viết có thể không chuẩn mực nhưng hy vọng sẽ cung cấp thêm cho các bạn lượng kiến thức nhất định. Chúc các bạn học tập vui vẻ!
Mệnh đề tập hợp -