Quy tắc đếm: Quy tắc cộng và quy tắc nhân

Bài viết dưới đây, tôi sẽ giới thiệu đến các bạn 2 quy tắc đếm lớp 11 là quy tắc cộng và quy tắc nhân. Đây là nội dung khởi đầu chương II tổ hợp và xác suất. Đồng thời tôi cũng chỉ cho các bạn cách phân biệt hai quy tắc này. Theo dõi bài viết dưới đây nhé!

QUY TẮC ĐẾM: QUY TẮC CỘNG

Giả sử chúng ta có một công việc có thể chia nhỏ ra thành hai công việc tạm gọi là việc 1 và việc 2. Sao cho mỗi cách thực hiện công việc 1 hay mỗi cách thực hiện của công việc 2  đều khiến 1 cách công việc ban đầu được hoàn thành. Mỗi cách của công việc 1 không trùng lặp cách của công việc 2 và ngược lại. Giả sử công việc 1 có m cách thực hiện. Công việc 2 có n cách thực hiện. Thì công việc ban đầu có m+n cách thực hiện. Quy tắc này có thể áp dụng tương tự cho việc chia nhỏ ra nhiều hơn 2 công việc.

Ví dụ:

Trong 1 lớp học có 11 học sinh nam và 22 học sinh. Có bao nhiêu cách chọn ra một học sinh.

Lời giải:

Việc chọn ra 1 học sinh có thể chia ra làm  hai công việc. Công việc 1 là chọn ra 1 học sinh nữ. Công việc 2 là chọn ra một học sinh nam. Dễ dàng thấy cách chia như vậy thỏa mãn điều kiện của quy tắc cộng. Hơn nữa công việc 1 có 22 cách. Công việc 2 có 11 cách. Vậy công việc chọn ra 1 học sinh có 11+22=33 cách.

Chắc hẳn các bạn đọc đến đây cho rằng quy tắc cộng rất dễ. Không có gì để bận tâm. Nhưng đây chỉ là ví dụ với việc phân chia công việc đơn giản. Còn với công việc phức tạp hơn việc phân chia này lại rất quan trọng. Tới phần tổ hợp các bạn sẽ thấy ý nghĩa của quy tắc này nhiều hơn.

QUY TẮC ĐẾM: QUY TẮC NHÂN

Giả sử chúng ta có một công việc có thể chia nhỏ ra thành hai công việc tạm gọi là việc 1 và việc 2. Sao cho mỗi cách thực hiện công việc 1 đều cần 1 cách thực hiện của công việc 2 để hoàn thành 1 cách của công việc ban đầu. Giả sử công việc 1 có m cách thực hiện. Công việc 2 có n cách thực hiện. Thì công việc ban đầu có m.n cách thực hiện. Quy tắc này cũng có thể áp dụng tương tự cho việc chia nhỏ ra nhiều hơn 2 công việc.

Ví dụ:

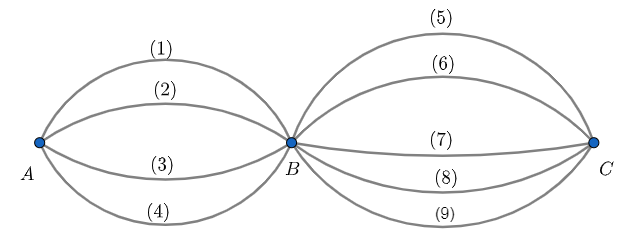
Một người đi từ A đến C cần phải đi qua B. Từ A đến B có 4 con đường. Từ B đến C có 5 con đường. Hỏi có bao nhiêu cách để người đó đi từ A đến C mà chỉ đi qua B đúng 1 lần?

Lời giải:

Ta chia việc đi từ A đến C thành 2 việc. Việc 1 đi từ A đến B. Việc 2 đi từ B đến C. Với mỗi cách đi từ A đến B ta cần 1 cách đi từ B đến C để hoàn thành việc đi từ A đến C. Do đó 2 việc trên thỏa mãn quy tắc nhân. Hơn nữa việc 1 có 4 cách thực hiện. Việc 2 có 5 cách thực hiện. Do đó có 4.5=20 cách đi từ A tới C.

Chúc các bạn học giỏi và thành công!

Xem thêm:

Chuyên đề tổ hợp xác suất P1: Đếm số tự nhiên

Bài tập quy tắc đếm lớp 11 có lời giải