Những bí quyết về chu vi và diện tích hình thoi

Trong chương trình lớp 4, học sinh sẽ được học về chu vi và diện tích của hình thoi. Qua việc học này, họ sẽ phát triển kỹ năng logic, rèn luyện khả năng tính toán và giải quyết vấn đề một cách chính xác. Công thức tính chu vi và diện tích hình thoi sẽ giúp trẻ hiểu rõ hơn về hình học và áp dụng được trong các bài toán thực tế. Ngoài ra, việc sử dụng các ứng dụng toán học như Monkey Math cũng giúp trẻ học toán một cách vui nhộn và đầy hứng thú.

Content

Cách tính chu vi hình thoi lớp 4 là gì?

Để tính chu vi của hình thoi, ta cần biết độ dài của các cạnh của hình thoi. Ví dụ, nếu cạnh của hình thoi có độ dài a, ta có:
Chu vi = a + a + a + a = 4a

Vậy chu vi của hình thoi là 4 lần độ dài của một cạnh. Để tính chu vi, chúng ta cần biết độ dài của các cạnh của hình thoi và thực hiện phép nhân để tính toán kết quả cuối cùng.

Để tránh nhầm lẫn và tính toán sai, hãy chắc chắn rằng bạn đã chọn đúng đơn vị đo lường cho cạnh của hình thoi và thực hiện phép tính một cách chính xác. Chúc bạn thành công trong việc tính toán chu vi của hình thoi!

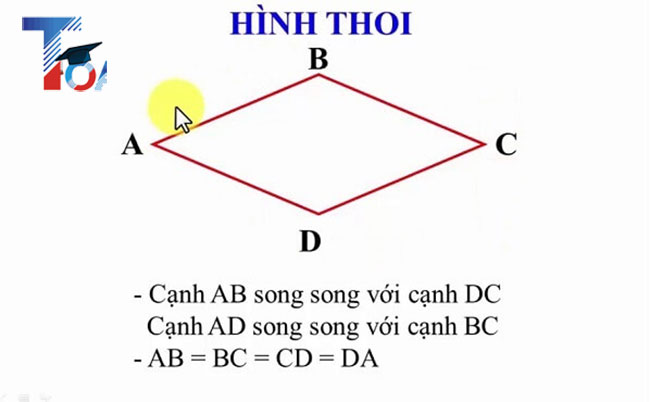
Hình thoi: Định nghĩa và đặc điểm của hình thoi

Hình thoi là một dạng hình học có những đặc điểm đặc trưng như cạnh bằng nhau, có đường chéo cắt nhau vuông góc và các góc đối diện bằng nhau. Việc tính toán diện tích và chu vi của hình thoi cũng rất đơn giản với các công thức đã nêu trên. Với kiến thức về hình thoi, chúng ta có thể áp dụng vào thực tế như trong việc xây dựng, chế tạo hay thiết kế các sản phẩm. Đây là một khái niệm không chỉ quan trọng mà còn cần thiết đối với việc giáo dục và học tập.

Cách tính chu vi hình thoi

Công thức tính chu vi của một hình thoi được tính bằng công thức chu vi = 4 x độ dài cạnh. Điều này có nghĩa là để tính chu vi của hình thoi, ta cần nhân độ dài của một cạnh với số 4.

Ví dụ, nếu cho một hình thoi có độ dài các cạnh bằng nhau và độ dài mỗi cạnh là 6 cm, ta có thể tính chu vi của hình thoi này như sau:
Chu vi = 4 x 6 = 24 cm.

Vậy, chu vi của hình thoi này sẽ là 24 cm. Điều này chứng minh rằng công thức chu vi = 4 x độ dài cạnh đúng với bất kỳ hình thoi nào có các cạnh bằng nhau.

Ví dụ tính chu vi của một hình thoi

Ngoài ra, để tính diện tích của một hình thoi, chúng ta có thể sử dụng công thức: Diện tích = Đường chéo dài x Đường chéo ngắn / 2.
Với hình thoi ABCD trong ví dụ trên, nếu đường chéo dài là 6 cm và đường chéo ngắn là 4 cm, ta có thể tính diện tích như sau:
Diện tích = 6 cm x 4 cm / 2 = 12 cm².
Vậy diện tích của hình thoi trong ví dụ này là 12 cm².

Như vậy, thông qua các công thức tính chu vi và diện tích của hình thoi, chúng ta có thể dễ dàng tính toán các thông số của hình thoi dựa trên độ dài các cạnh và đường chéo của nó.

Chu vi và diện tích hình thoi – Học toán tư duy ở lớp 4 trên KES

Diện tích của hình thoi là một trong những kiến thức cơ bản được học trong toán học. Để tính diện tích của hình thoi, chúng ta cần biết công thức tính diện tích của hình thoi.

Diện tích của hình thoi có thể được tính bằng công thức: Diện tích = (đường chéo lớn x đường chéo nhỏ)/2.

Ví dụ, giả sử ta có một hình thoi có độ dài đường chéo lớn là 8 cm và độ dài đường chéo nhỏ là 6 cm. Để tính diện tích của hình thoi này, ta sử dụng công thức trên: Diện tích = (8 x 6)/2 = 24 cm².

Cách tính diện tích hình thoi

Để tính diện tích của một hình thoi, ta sử dụng công thức S = (đường chéo dài x đường chéo ngắn)/2. Đầu tiên, ta xác định đường chéo dài và đường chéo ngắn của hình thoi. Tiếp theo, tính tích của hai đường chéo và chia cho 2 để có diện tích của hình thoi đó.

Ví dụ, hình thoi ABCD có đường chéo dài là 8 cm và đường chéo ngắn là 6 cm. Áp dụng công thức, ta có S = (8 x 6)/2 = 48/2 = 24 cm². Vậy, diện tích của hình thoi ABCD là 24 cm².

Như vậy, để tính diện tích của một hình thoi, ta chỉ cần biết hai đường chéo của nó và sử dụng công thức đơn giản trên.

Ví dụ tính diện tích của hình thoi

Để tính diện tích của một hình thoi, chúng ta có thể sử dụng công thức là nửa tích của hai đường chéo nhân với nhau.

Ví dụ: Cho một hình thoi có đường chéo chính dài 10 cm và đường chéo phụ dài 6 cm.

Bước 1: Tính độ dài các cạnh của hình thoi theo công thức Pythagoras.
– Gọi a, b, c, d lần lượt là độ dài các cạnh của hình thoi.
– Ta có a^2 + b^2 = 10^2 và c^2 + d^2 = 6^2.
– Giải hệ phương trình ta được a = b = √64 và c = d = √36.
– Vậy a = b = 8 cm và c = d = 6 cm.

Bước 2: Tính diện tích của hình thoi.
– Diện tích = (10 6) / 2 = 30 cm^2.

Vậy, diện tích của hình thoi trong ví dụ này là 30 cm^2.

Tìm mối liên hệ giữa chu vi và diện tích của hình thoi

Ví dụ, nếu độ dài đường chéo chính d1 là 10 đơn vị và độ dài đường chéo phụ d2 là 6 đơn vị, ta có thể tính được chu vi và diện tích của hình thoi như sau:

– Chu vi = 2 (10 + 6) = 32 đơn vị
– Diện tích = (10 6) / 2 = 30 đơn vị vuông

Do đó, trong trường hợp này, chu vi của hình thoi là 32 đơn vị và diện tích là 30 đơn vị vuông. Đây chính là một ví dụ cụ thể về mối liên hệ giữa chu vi và diện tích của một hình thoi dựa trên công thức đã nêu trên.

Toán lớp 4: Tìm diện tích hình thoi

Bạn đã bao giờ tự hỏi làm thế nào để tính chu vi và diện tích của hình thoi chưa? Nếu chưa, hãy cùng nhau tìm hiểu cách làm này để trở thành chuyên gia toán học nhé!

Đầu tiên, bạn cần biết rằng chu vi của hình thoi được tính bằng cách cộng tổng độ dài của tất cả các cạnh lại với nhau. Ví dụ, nếu bạn biết chiều dài một cạnh của hình thoi là a, thì chu vi của hình thoi sẽ là 4a (vì hình thoi có 4 cạnh bằng nhau).

Tiếp theo, để tính diện tích của hình thoi, bạn chỉ cần nhân độ dài của một đường chéo với chiều cao tương ứng và chia cho 2. Ví dụ, nếu chiều dài đường chéo dài nhất của hình thoi là d và chiều cao tương ứng là h, thì diện tích của hình thoi sẽ là (d x h) / 2.

Một số ví dụ thực tế giúp bạn nắm bắt nhanh chóng cách tính chu vi và diện tích của hình thoi là:

1. Một học sinh vẽ một hình thoi có chiều dài mỗi cạnh là 5cm. Hãy tính chu vi của hình thoi đó.
2. Một công ty xây dựng muốn làm một khu vườn hình thoi có đường chéo dài 10m và chiều cao 8m. Hãy tính diện tích của khu vườn đó.

Nhớ áp dụng những công thức và ví dụ trên để trở thành chuyên gia toán học nhé! Hãy thực hành nhiều và không ngần ngại khi gặp phải các bài toán mới. Chúc bạn may mắn!

Chu vi và diện tích của một hình thoi: Cái nào lớn hơn?

Hình thoi là một hình tứ giác có tất cả các cạnh bằng nhau và các góc bằng nhau. Để tính chu vi của hình thoi, chúng ta có thể sử dụng công thức: chu vi = 4 x cạnh. Còn để tính diện tích của hình thoi, chúng ta có thể sử dụng công thức: diện tích = cạnh x chiều cao.

Ví dụ, nếu cạnh của hình thoi là 10cm, thì chu vi sẽ là 40cm và diện tích sẽ là 50cm2. Nhưng nếu cạnh của hình thoi là 20cm, thì chu vi sẽ là 80cm và diện tích sẽ là 200cm2.

Vì vậy, chỉ khi biết kích thước cụ thể của hình thoi, chúng ta mới có thể so sánh giá trị của chu vi và diện tích. Không thể nói rằng chu vi lớn hơn diện tích hoặc ngược lại mà phải xem xét từng trường hợp cụ thể.

Các ứng dụng thực tiễn của hình thoi

Với những ứng dụng đa dạng như vậy, hình thoi không chỉ là một hình dạng đơn giản mà còn là một phần không thể thiếu trong cuộc sống hàng ngày của chúng ta. Việc hiểu và áp dụng hình thoi đúng cách không chỉ giúp chúng ta có thể tạo ra những sản phẩm đẹp mắt và sáng tạo mà còn giúp chúng ta vận dụng kiến thức toán học vào thực tế một cách linh hoạt và sáng tạo.

Nếu bạn là một người yêu thích nghệ thuật, thiết kế, xây dựng hoặc đơn giản là muốn nâng cao kiến thức toán học của mình, hãy khám phá và tìm hiểu thêm về hình thoi và những ứng dụng thực tiễn của nó. Chắc chắn rằng bạn sẽ có những trải nghiệm thú vị và bổ ích từ việc khám phá vẻ đẹp và tính ứng dụng của hình thoi trong cuộc sống hàng ngày.

Hướng dẫn vẽ hình thoi và tính chu vi, diện tích bằng công thức

Để vẽ một hình thoi, bạn cần làm theo các bước sau đây:
1. Vẽ một đoạn thẳng AB là cạnh của hình thoi.
2. Đặt compa ở điểm A và vẽ một góc 120 độ.
3. Đặt compa ở điểm B và vẽ một góc 120 độ.
4. Đặt compa ở điểm A và vẽ một đoạn thẳng có độ dài bằng đoạn thẳng AB.
5. Kết nối các điểm A, B, C, D để tạo thành hình thoi ABCD.

Để tính chu vi của hình thoi, sử dụng công thức: chu vi = 4 x độ dài cạnh.
Để tính diện tích của hình thoi, sử dụng công thức: diện tích = (độ dài cạnh x độ dài đường chéo) / 2.

Hy vọng thông tin này giúp bạn hiểu cách vẽ và tính toán hình thoi. Hãy thực hành để trở thành một người vẽ giỏi nhé!

Blog Toán Học -