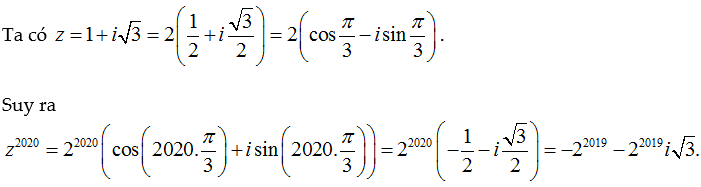Dạng lượng giác của số phức và ứng dụng
Dạng lượng giác của số phức là gì? Có phải dạng lượng giác số phức có thể ứng dụng được trong các đề thi THPT QG hay không? Các em cùng đọc bài viết dưới đây để tìm hiểu nhé. Nhưng các em hãy bình tĩnh. Trước tiên chúng ta cần phải có 2 khái niệm argument và mô đun của số phức đã.
Content
ARGUMENT VÀ MÔ ĐUN CỦA SỐ PHỨC
1. ARGUMENT CỦA SỐ PHỨC
Trong từng sách khác nhau thì định nghĩa về argument của số phức có thể khác nhau. Lý do là khi ta quay điểm biểm biểu diễn số phức quanh gốc tọa độ 1 vòng thì giá trị của số phức không đổi. Vì vậy khi các em đọc bài viết này và các bài viết trên trang khác. Nếu có sự khác nhau về khái niệm argument của số phức thì không lấy làm lạ nhé.
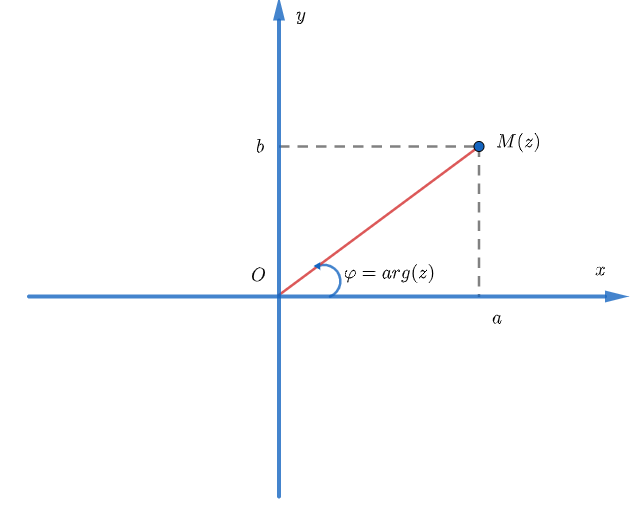
Giả sử M(z) là điểm biểu diễn số phức z. Argument của số phức z (z≠0) (ký hiêu: Arg(z) chữ A viết in hoa) là góc định hướng giữa chiều dương của trục thực và tia OM(z) thỏa mãn -π< Arg(z)≤π. Các bài toán trong bài viết này sử dụng quy ước argument như trên. Các em cùng lưu ý nhé.
Rõ ràng nếu z=a+bi (a,b∈R) thì Arg(z)=Arctan(b/a).
2. MÔ ĐUN CỦA SỐ PHỨC
Với mỗi số phức z=a+bi (a,b∈R) thì mô đun của số phức z là một số thực ký hiệu là |z| và được tính theo công thức
Về mặt biểu diễn hình học thì mô đun của số phức z chính là khoảng cách từ điểm M(z) đến gốc tọa độ. Hay nói cách khác |z|=OM(z).
DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC
Với mỗi số phức z =a+bi (a,b∈R). Ta có: z=r(cosφ+isinφ) là dạng lượng gιác của số phức z. Trong đó r là mô đun của z, φ là Argument của z.
Ví dụ:
Tìm dạng lượng giác của z=1+i.
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
ỨNG DỤNG CỦA SỐ PHỨC DẠNG LƯỢNG GIÁC
Dạng lượng giác cùng dạng lũy thừa số phức hiện nay không còn được giảng dạy trong chương trình sách giáo khoa cơ bản. Tuy nhiên với hình thức thi trắc nghiệm thì không ai cấm chúng ta nghiên cứu và sử dụng nó trong giải toán.
Một trong các ứng dụng của số phức dạng lượng gιác là tính lũy thừa số phức bậc cao. Công thức sau đây gọi là công thức Moivre:
Ví dụ minh họa:
Lời giải:
Xem thêm:
Số Phức -