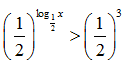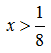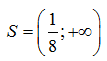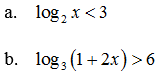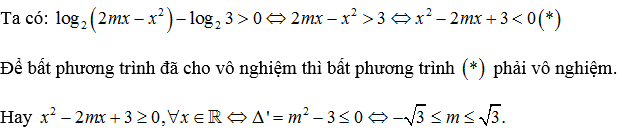Bất phương trình logarit tổng hợp
Giải bất phương trình logarit như thế nào? Có những dạng nào? Bài viết dưới đây tôi sẽ giới thiệu đến các bạn các dạng bất phương trình lôgarit từ cơ bản đến vận dụng. Bên cạnh đó sẽ có 1 số bài tập có hướng dẫn giải để áp dụng. Hãy đọc bài viết để tìm hiểu nhé.
I. BẤT PHƯƠNG TRÌNH LOGARIT CƠ BẢN
Với cơ số a dương và khác 1, các bất phương trình có 1 trong các dạng sau gọi là bất phương trình lôgarit cơ bản:
Với mỗi dạng bất phương trình trên, tùy thuộc vào cơ số cách giải có điểm khác nhau. Tuy nhiên các bạn có thể nhớ 1 điểm chung là giá trị của biến x phải dương để logarit xác định. Đồng thời các bất phương trình cơ bản này đều có thể giải theo kiểu mũ hóa 2 vế với cơ số a. Và khi mũ hóa như vậy thì a>1 bất phương trình sẽ không đổi chiều. Ngược lại với 0<a<1 thì bất phương trình sẽ đổi chiều. Cách nhớ như thế sẽ giúp các bạn không cần nhớ máy móc công thức.
Sau đây tôi sẽ phân tích chi tiết các bước qua 1 ví dụ nhé.
Ví dụ:
Giải bất phương trình sau:
Hướng dẫn:
Trước hết ta có điều kiện x>0.
Mũ hóa 2 vế với cơ số 1/2 ta được bất phương trình đảo chiều so với chiều ban đầu.
Áp dụng công thức sau cho vế trái
Ta được:
Kết hợp với điều kiện x>0(chú ý ở điểm này khác với giải phương trình lôgarit) ta được tập nghiệm là
Hướng dẫn chi tiết là vậy. Nhưng khi các bạn đã hiểu thì hãy viết cho gọn lại nhé. Các bạn đọc ở chỗ khác có thể thấy hướng dẫn kiểu khác. Tuy nhiên theo hướng dẫn tôi trình bày ở trên là 1 cách an toàn cho các bạn có học lực trung bình.
Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit
Chúng ta hay luyện tập thêm thông qua 2 bất phương trình sau:
Ví dụ:
Giải các bất phương trình sau
Lời giải:
II. BẤT PHƯƠNG TRÌNH LOGARIT CHỨA THAM SỐ
Với bất phương trình lôgarit có chứa tham số thì câu hỏi khá đa dạng. Trong đó câu hỏi tìm m để bất phương trình có nghiệm thỏa mãn điều kiện cho trước khá phổ biến.
Lưu ý chung đối với dạng toán này là khi biến đổi ta cần biến đổi trương đương thì mới đánh giá được miền nghiệm.
Chúng ta cùng xét một ví dụ sau:
Ví dụ:
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit
Trên đây là cách giải bất phương trình loogarit cơ bản và 1 vài lưu ý khi giải bất phương trình lôgarit có chứa tham số. Chúc các bạn thành công!
Lũy Thừa - Lôgarit -