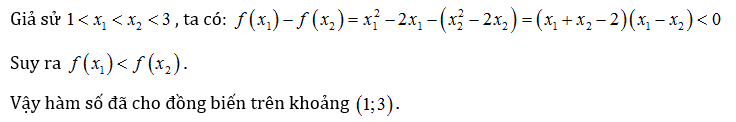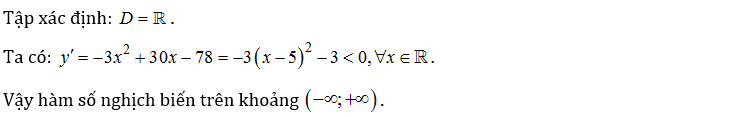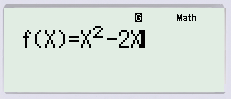Tính đơn điệu của hàm số xét như thế nào?

Xét tính đơn điệu của hàm số hay tìm khoảng đơn điệu của hàm số là một nội dung quan trọng trong chương trình lớp 12. Đồng thời cũng là một dạng toán có tần suất xuất hiện cao trong các đề thi THPTQG. Vì vậy ôn tập tốt dạng toán này là một việc hết sức quan trọng. Bài viết giới thiệu phương pháp xét tính đơn điệu của hàm số thông qua bốn cách: Dùng định nghĩa, dùng đạo hàm, dùng máy tính bỏ túi, nhớ một số hàm số thường gặp. Tùy vào bài toán cụ thể các em có thể lựa chọn phương pháp phù hợp để giải.

I. XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ BẰNG ĐỊNH NGHĨA

Trước khi có công cụ đạo hàm để xét tính đơn điệu thì chúng ta sử dụng phương pháp này.

Định nghĩa hàm số đơn điệu:

Chứng minh rằng hàm số y=f(x)=x²-2x đồng biến trên khoảng (1;3).

Lời giải:

II. XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ BẰNG ĐẠO HÀM

Dùng đạo hàm là phương pháp xét tính đơn điệu của hàm số lớp 12. Với công cụ đạo hàm ta có thể xử lý nhanh lớp các hàm số có đạo hàm. Tất nhiên nhược điểm của nó là không xử lý được các hàm số không có đạo hàm. Nhưng như vậy là quá đủ cho toán THPT rồi.

Ta có mối liên hệ giữa tính đơn điệu của hàm số và đạo hàm được thể hiện qua định lý sau:

Lưu ý là dấu bằng của đạo hàm trong định lý chỉ được xảy ra tại hữu hạn điểm. Nếu dấu bằng xảy ra tại vô số điểm thì tập vô số điểm đó phải đếm được. Các bạn học sinh THPT cũng không cần quan tâm quá sâu vào khái niệm tập đếm được đâu. Hàm số đồng biến nghịch biến và đồng biến trên đoạn và nửa khoảng chúng ta cũng có định lý hoàn toàn tương tự. Các bạn có thể tham khảo thêm trong SGK nâng cao.

Từ định lý trên ta có các bước để xét sự đơn điệu của hàm số y=f(x) như sau:

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y’=f'(x).

Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

Bước 4: Lập bảng biến thiên. Nếu dễ đánh giá được đạo hàm thì có thể bỏ qua bước này.

Bước 5: Kết luận.

Chú ý: Đối với bài toán trắc nghiệm, ta có thể sử dụng Phương pháp sử dụng MTCT.

Bộ đề thi Online các dạng có giải chi tiết: Hàm số

Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số y=-x³+15x²-78x-3.

Lời giải:

III. DÙNG MÁY TÍNH BỎ TÚI XÉT SỰ ĐƠN ĐIỆU CỦA HÀM SỐ

Dùng máy tính bỏ túi hay thường được gọi là Casio (có lẽ do mọi người quen gọi như vậy nên mình cũng xin phép gọi tắt là Casio cho tiện mặc dù mình dùng máy Vinacal :)). Xin nhắc lại rằng hầu hết các thủ thuật liên quan đến Casio đều mang tính ước lượng không thay thế cho chứng minh được. Và trong câu hỏi trắc nghiệm ta có thể dùng để loại trừ phương án sai.

Hàm số y=f(x)=x²-2x đồng biến trong khoảng nào trong các khoảng sau đây?

A. (−∞;1).                         B. (0;2).                       C. (1;3).                        D. (−2;+∞)

Lời giải:

Ta vào chế độ MODE 7 1 hàm số (Cài đặt 1 hàm số ở shift mode ↓ 5. Các bạn có thể yêu cầu cách bấm chi tiết bằng cách để lại bình luận ở dưới bài viết)

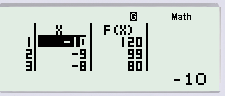
Để xét phương án A ở phần START ta chọn chẳng hạn −10, END ta chọn 1, STEP ta chọn 1.

Ở bảng giá trị của F(X) ta thấy biến thì tăng trong khi giá trị lại giảm. Do đó hàm số không thể đồng biến trên khoảng ở phương án A được. Vậy ta loại phương án A. Cứ thực hiện như vậy đến khi ta loại được ba phương án còn lại phương án C là đáp án. Chọn C.

Chúc các bạn thành công!

Xem thêm:

Hàm số liên tục và một số dạng toán thường gặp

Hàm số đồng biến trên R hàm số nghịch biến trên R

Tìm m để hàm số đồng biến nghịch biến trên khoảng