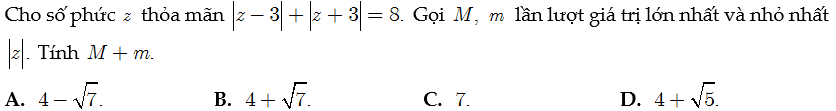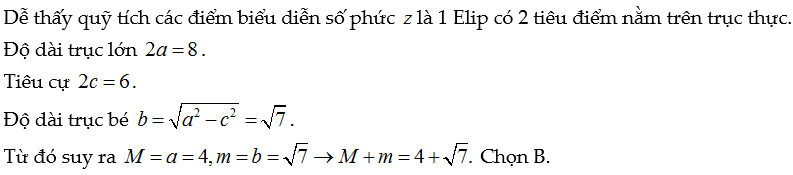Tìm tập hợp điểm biểu diễn số phức như thế nào ?
Tìm tập hợp điểm biểu diễn số phức là 1 dạng toán hay trong chuyên đề SỐ PHỨC. Làm thế nào để làm dạng toán này một cách nhanh nhất. Đọc bài viết dưới đây sẽ giúp các em có cách nhìn tổng quan về dạng toán này. Cũng như giúp các em có phương pháp giải tốt nhất có thể. Cùng theo dõi bài viết nhé!
Content
BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
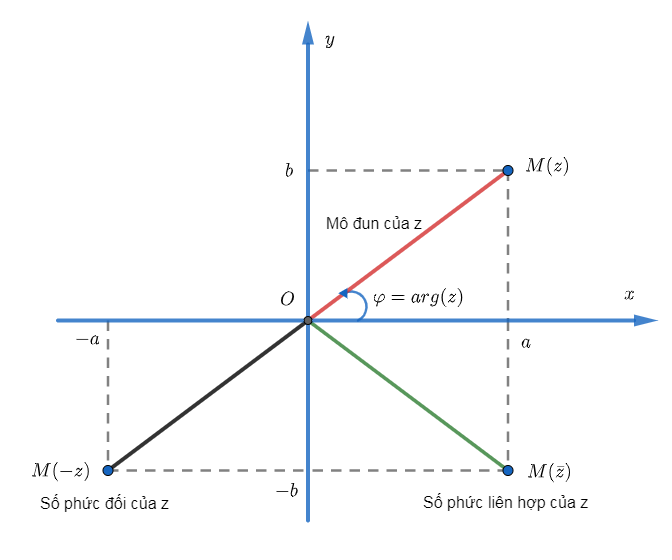
Như chúng ta đã biết từ bài viết trước, mỗi số phức z=a+bi(a,b∈R) được đặt tương ứng với một điểm M(z)=(a;b) trên mặt phẳng tọa độ là 1 song ánh. Các khái niệm trong tập số phức được tương ứng lên mặt phẳng như:
- Phần thực của z là hoành độ của điểm M(z).
- Phần ảo của z là tung độ của điểm M(z).
- Mô đun của z là độ dài đoạn OM(z). Trong đó O là gốc tọa độ.
- Số phức liên hợp của z được biểu diễn bởi điểm đối xứng với M(z) qua trục thực.
- …
Rõ ràng với sự tương ứng như vậy thì 1 phương trình, hệ phương trình, bất phương trình (phức) cũng sẽ được tương ứng với một hình nào đó trên mặt phẳng phức. Vì vậy mà chúng ta có 1 lớp các bài toán xác định tập hợp các điểm trong mặt phẳng phức thỏa mãn điều kiện cho trước. Để chuẩn bị tốt cho dạng toán này các em cần ghi nhớ một số hình biểu diễn cơ bản và thường gặp dưới đây.
TÌM TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC Z THỎA MÃN
|z-(a+bi)|=r
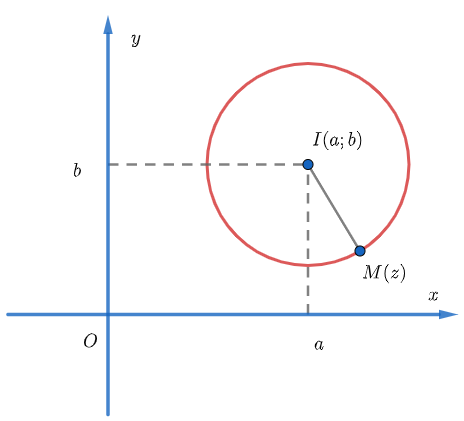
Tập hợp các điểm biểu diễn số phức z thỏa mãn phương trình |z-(a+bi)|=r là đường tròn tâm I(a;b) bán kính r.
Thực vậy, điểm M(z) biểu diễn cho số phức z thì điểm I(a;b) biểu diễn cho số phức a+bi. Do đó |z-(a+bi)| được biểu diễn bởi đoạn IM(z). Vậy quỹ tích các điểm biểu diễn cho số phức z thỏa mãn phương trình |z-(a+bi)|=r là đường tròn tâm I(a;b) bán kính r.
Ví dụ minh họa:
Cho số phức z thỏa mãn |z+2-3i|=3 là một đường tròn. Biết tập hợp các điểm biểu diễn số phức w=(3+4i)z+3-5i là một đường tròn. Tìm tâm và bán kính của đường tròn đó.
Phân tích: Đối với bài toán dạng này ta thường thêm bớt trong phương trình của w để xuất hiện giả thiết. Sau đó lấy mô đun 2 vế.
Lời giải:
Cách 1.
Ta có:
w=(3+4i)z+3-5i⇔ w=(3+4i)(z+2-3i-2+3i)+3-5i
⇔ w=(3+4i)(z+2-3i)+(3+4i)(-2+3i)+3-5i⇔w+15+4i= (3+4i)(z+2-3i)
Lấy mô đun 2 vế ta được:
|w+15+4i|=| 3+4i|.| z+2-3i|⇔ |w+15+4i|=15.
Vậy các điểm biểu diễn số phức w là đường tròn tâm I(-15;-4) bán kính R=15.
Cách 2. (Siêu nhanh)
Chúng ta lưu ý rằng nếu M(z) biểu diễn cho số phức z. Thì điểm M(z+(a+bi)) có được bằng cách tịnh tiến M(z) theo véc tơ có tọa độ (a;b). Còn M(z.(a+bi)) có được bằng cách thực hiện phép quay tâm O điểm M(z) theo arg(a+bi). Sau đó vị tự tâm O tỉ số |a+bi|. Chúng ta cũng cần nhớ thêm rằng phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính, biến tâm thành tâm. Phép vị tự tỉ số k biến đường tròn bán kính R thành đường tròn bán kính |k|R, biến tâm thành tâm. Nói thì dài dòng vậy nhưng khi thực hiện lại khá nhanh. Thực vậy:
Tâm của đường tròn biểu diễn z là I(-2;3)→(3+4i)(-2+3i)+3-5i=-15-4i→Tâm đường tròn biểu diễn w là I(-15;-4).
Bán kính đường tròn biểu diễn z là 3→Bán kính đường tròn biểu diễn w là R=| 3+4i|.3=15.
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
Một số lưu ý:
- Các điểm biểu diễn cho số phức z thỏa mãn bất phương trình |z-(a+bi)|<r là hình tròn tâm I(a;b) bán kính r (không kể biên). Nếu có thêm dấu = thì kể cả biên.
- Các điểm biểu diễn cho số phức z thỏa mãn bất phương trình |z-(a+bi)|>r là phần ngoài hình tròn tâm I(a;b) bán kính r (không kể biên). Nếu có thêm dấu = thì kể cả biên.
- Các điểm biểu diễn cho số phức z thỏa mãn bất phương trình r<|z-(a+bi)|<R là hình vành khuyên giới hạn bởi hai đường tròn đồng tâm I(a;b) bán kính r và R.
TÌM TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC Z THỎA MÃN
|z-(m+ni)|+|z-(p+qi)|=2a
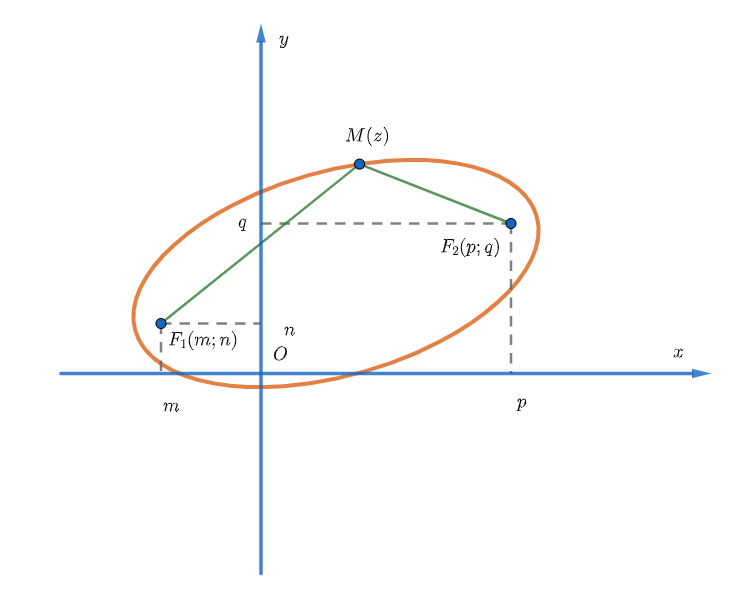
Các điểm biểu diễn số phức z thỏa mãn |z-(m+ni)|+|z-(p+qi)|=2a là đường Elip với hai tiêu điểm có tọa độ là F1(m;n) và F2(p;q). Độ dài trục lớn là 2a.
Ví dụ minh họa:
Lời giải:
Bộ đề thi Online các dạng có giải chi tiết: Số Phức
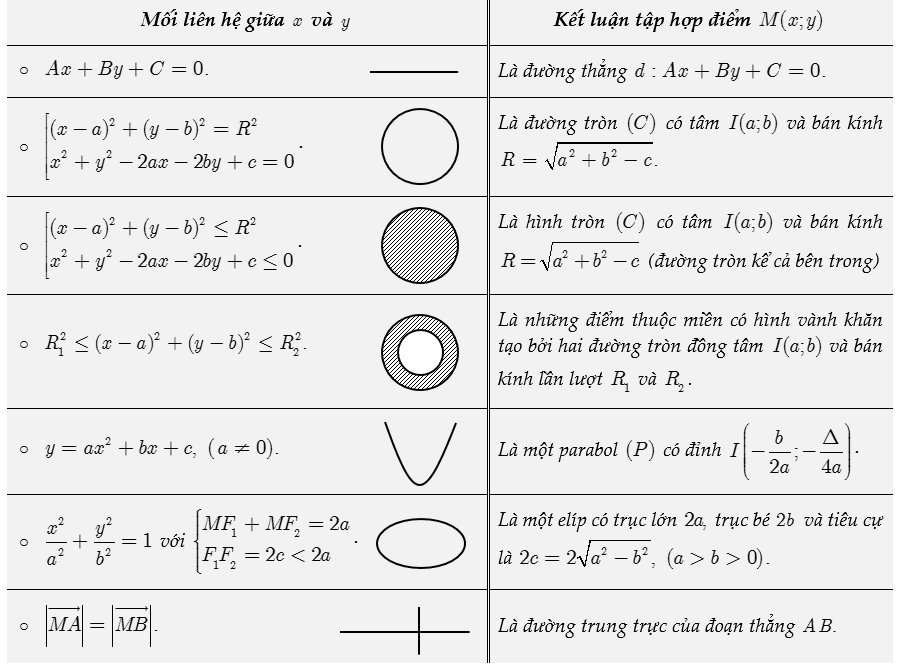
Trên đây là 2 hình biểu diễn số phức chúng ta thường gặp (đường tròn và Elip). Ngoài cách trên (nhanh) chúng ta có cách giải chung (cần biến đổi nhiều hơn) là giả sử z=x+yi (x,y∈R). Sau đó thay vào phương trình hay bất phương trình đã cho để biến đổi. Cuối cùng ta tiến hành nhận dạng phương trình đó là hình gì theo bảng sau:
Chúc các em thành công!
Xem thêm:
Modun số phức và các tính chất liên quan
Khái niệm lý thuyết tổng quan về số phức
Số Phức -