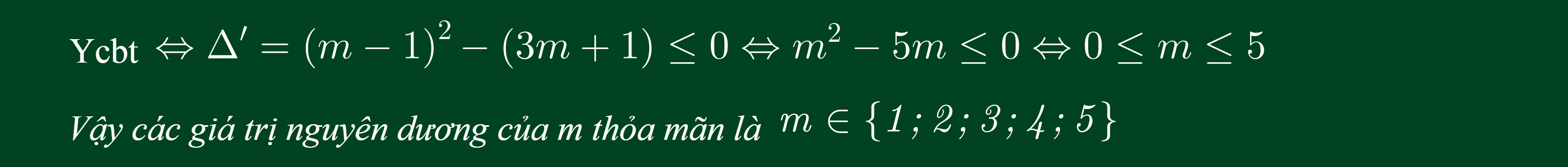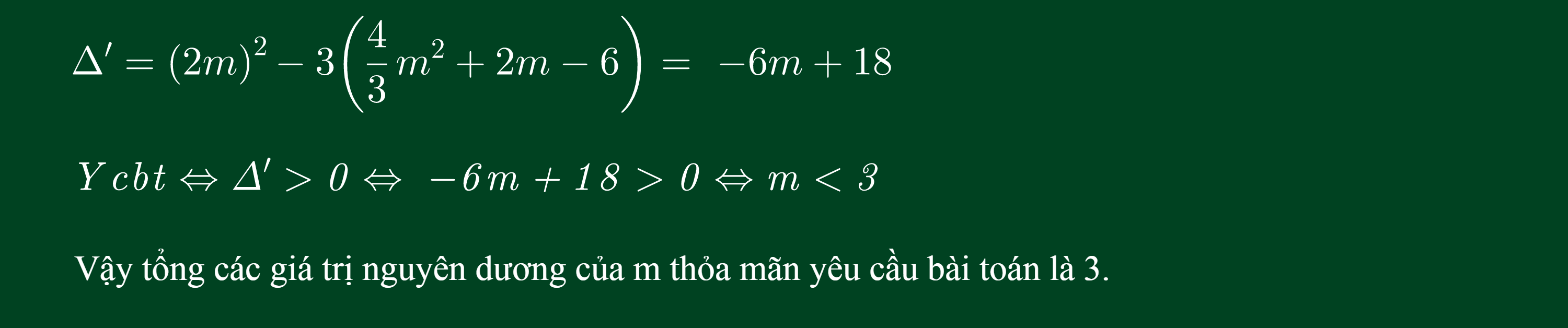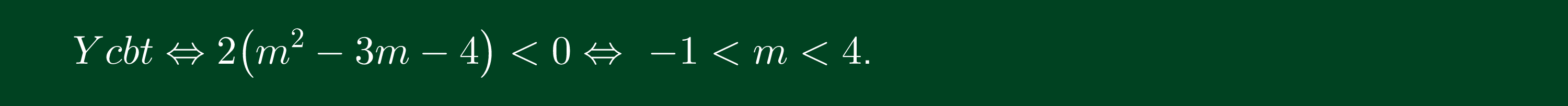Tìm m để hàm số không có cực trị như thế nào?

Tìm m để hàm số không có cực trị là một trong các dạng toán phổ biến của chủ đề HÀM SỐ. Trong bài viết này sẽ giới thiệu và hướng dẫn các em cách làm đối với các hàm số đa thức thường gặp là hàm đa thức bậc ba, hàm trùng phương bậc bốn.

…………………………………………………

Content

ĐIỀU KIỆN ĐỂ HÀM SỐ ĐA THỨC BẬC BA KHÔNG CÓ CỰC TRỊ

điều kiện để hàm số không có cực trị

Điều kiện để hàm số đa thức bậc ba không có cực trị

Ví dụ: Tìm các giá trị nguyên dương của m để hàm số y = \frac{1}{3} {x^3} + \left( {m - 1} \right){x^2} + \left( {3m + 1} \right)x + 2 không có cực trị.
Lời giải:

Ycbt $⇔\Delta ' = {\left( {m - 1} \right)^2} - \left( {3m + 1} \right) \le 0⇔{m^2} - 5m \le 0 \Leftrightarrow 0 \le m \le 5$

…………………………………..

ĐIỀU KIỆN ĐỂ HÀM SỐ ĐA THỨC BẬC BA CÓ CỰC TRỊ

Hàm số đa thức bậc ba có cực trị thì sẽ có hai cực trị. Trong đó có 1 cực đại và một cực tiểu. Do đó số cực trị và số điểm cực trị bằng nhau.

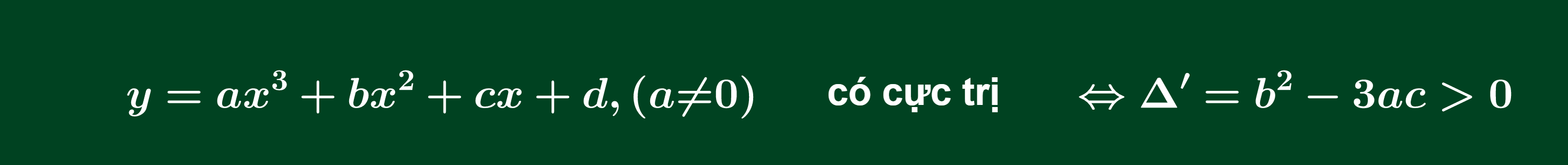
Điều kiện để hàm số đa thức bậc ba có cực trị

Điều kiện để hàm số đa thức bậc ba có cực trị

Ví dụ: Tính tổng tất cả các giá trị nguyên dương của tham số m để hàm số y = {x^3} - 2m{x^2} + \left( {\frac{4}{3}{m^2} - 2m + 3} \right)x - 6 có cực trị.

Lời giải:

………………………………..

Bộ đề thi Online các dạng có giải chi tiết: Cực trị của Hàm số

HÀM SỐ ĐA THỨC TRÙNG PHƯƠNG BẬC BỐN

Hàm số đa thức bậc chẵn thì không thể có trường hợp không có cực trị  được. Lúc nào nó cũng có ít nhất một cực trị. Với hàm số trùng phương bậc bốn ta có các trường hợp sau:

Trường hợp 1: Có đúng 1 cực trị

Điều kiện để hàm trùng phương có đúng một cực trị

Điều kiện để hàm trùng phương có đúng một cực trị

Ví dụ: Có bao nhiêu giá trị nguyên của m để hàm số y = {x^4} + 2\left( {1 - {m^2}} \right){x^2} - 3 có 1 điểm cực trị?

Lời giải:

Trường hợp 2: Có đúng ba điểm cực trị 

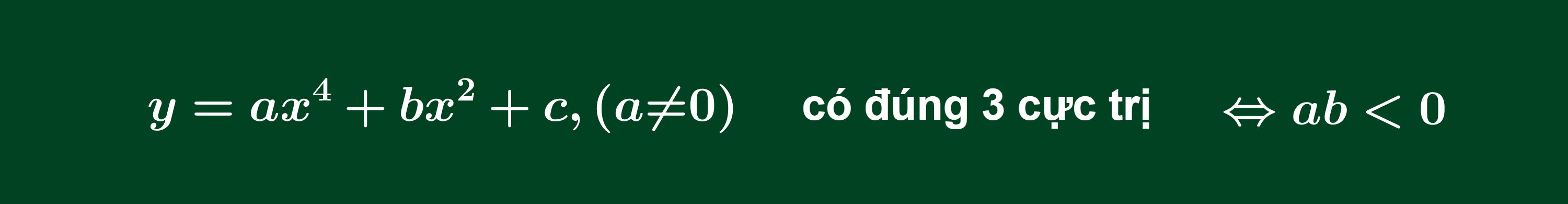
Điều kiện để hàm trùng phương có đúng 3 điểm cực trị

Điều kiện để hàm trùng phương có đúng 3 điểm cực trị

Lưu ý: Theo sách giáo khoa hiện hành thì trường hợp này có 2 cực trị và 3 điểm cực trị

Ví dụ: Tìm m để hàm số y = {x^4} + 2\left( {{m^2} - 3m - 4} \right){x^2} - 2m + 3 có 3 điểm cực trị.

Lời giải:

Đối với các hàm số khác thì chúng ta cần tìm điều kiện để đạo hàm không có nghiệm hoặc đạo hàm có nghiệm mà qua nghiệm đó đạo hàm không đổi dấu (nghiệm bội chẵn).

Đề thi Online có giải: [7-8] Tìm m để hàm số trùng phương có cực trị thỏa mãn điều kiện cho trước

Xem thêm:

Cực trị của hàm số – Phương pháp giải

 

Hàm số -