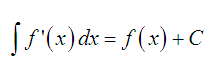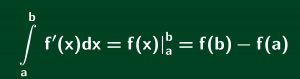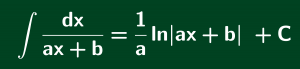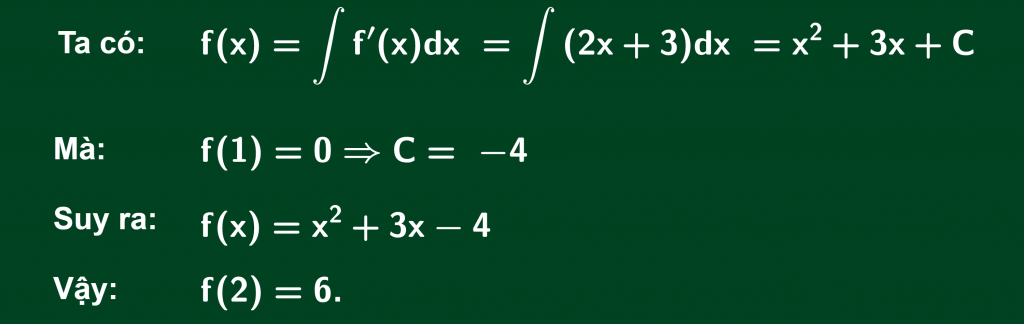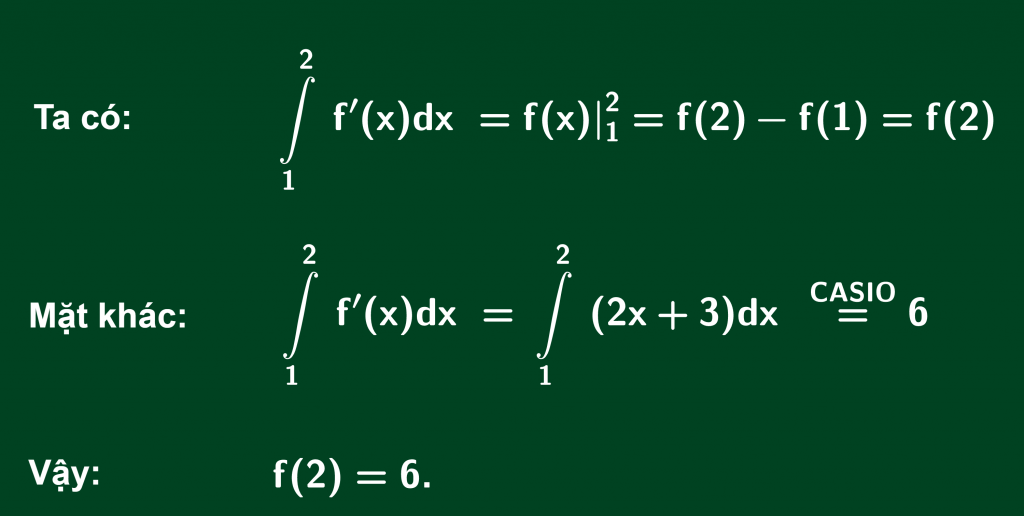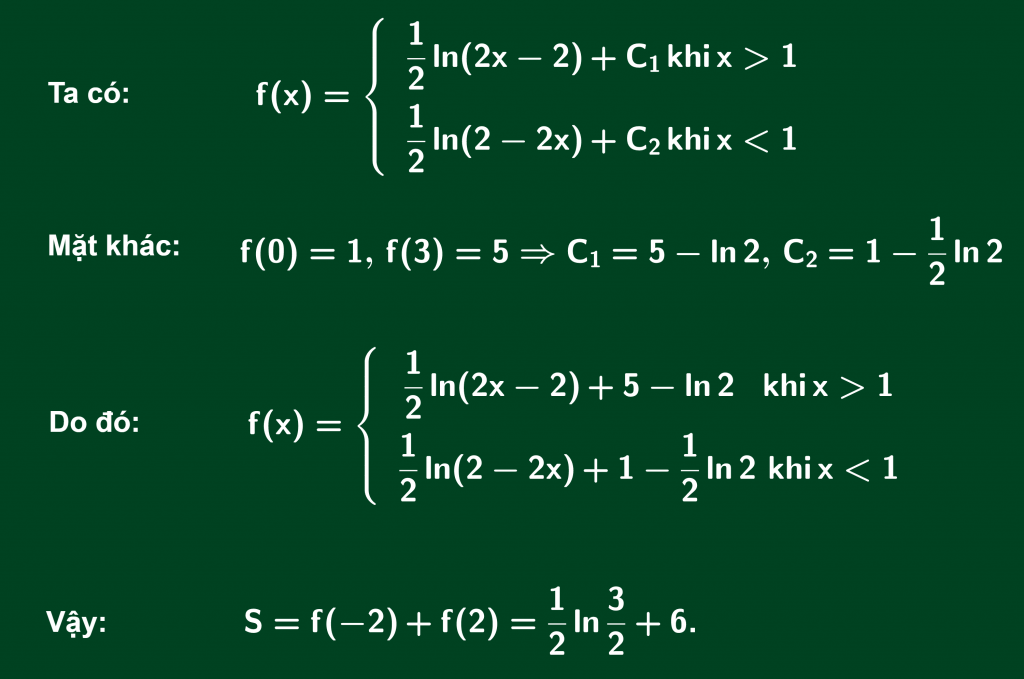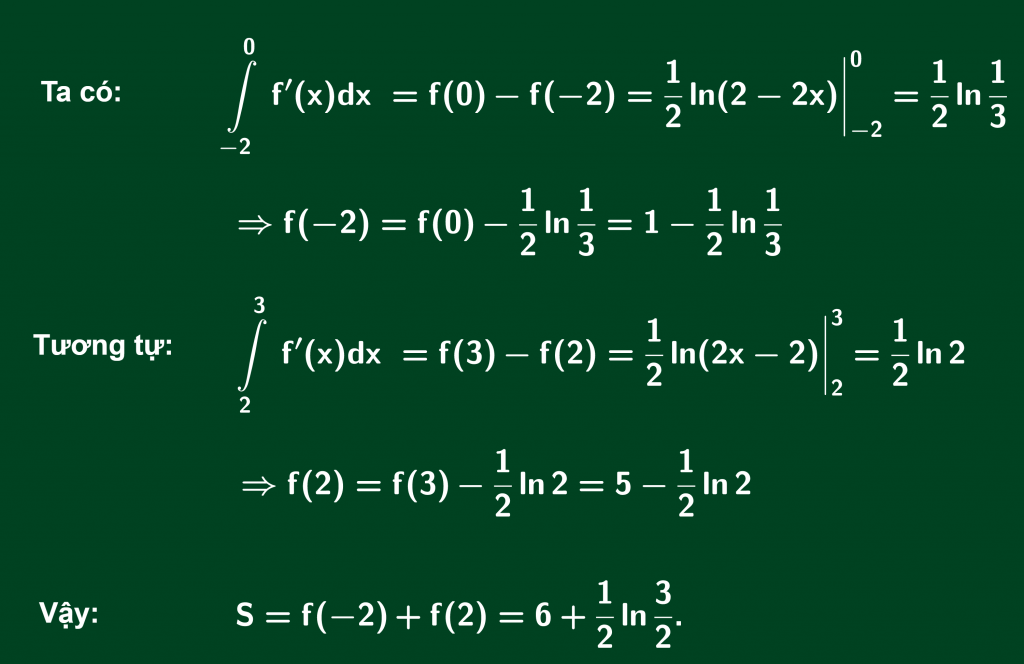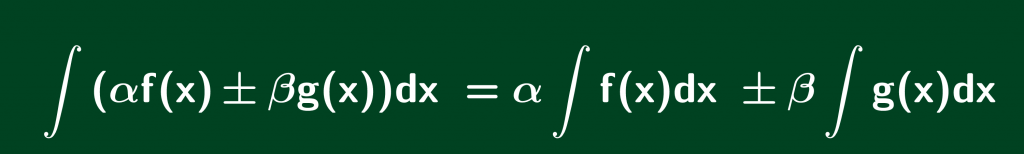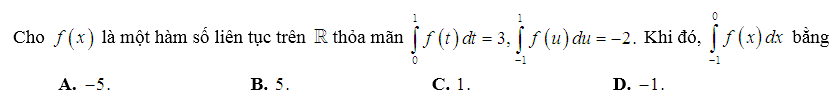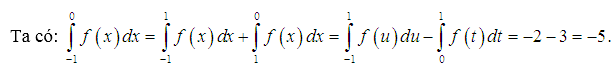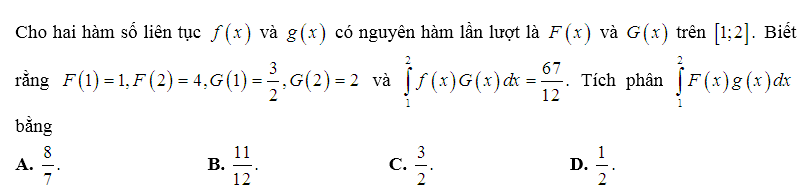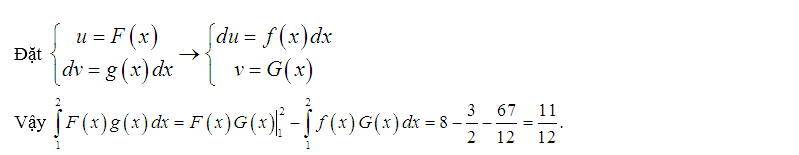Tích phân hàm ẩn – Lý thuyết và bài tập minh họa

Tích phân hàm ẩn là dạng tích phân mà ở đó hàm số bị ẩn đi. Tức là hàm số không được cho dưới dạng tường minh là một công thức. Sau đây chúng ta sẽ phân loại tích phân hàm ẩn theo các dạng: Cần sử dụng định nghĩa nguyên hàm, tích phân; sử dụng phương pháp đổi biến; sử dụng nguyên hàm và tích phân từng phần để các bạn dễ tiếp cận dạng toán này hơn nhé.

Content

1 TÍCH PHÂN HÀM ẨN SỬ DỤNG ĐỊNH NGHĨA NGUYÊN HÀM, TÍCH PHÂN
2 TÍCH PHÂN HÀM ẨN SỬ DỤNG TÍNH CHẤT CỦA NGUYÊN HÀM, TÍCH PHÂN
3 TÍCH PHÂN HÀM ẨN SỬ DỤNG PHƯƠNG PHÁP ĐỔI BIẾN SỐ
4 TÍCH PHÂN HÀM ẨN SỬ DỤNG PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN

TÍCH PHÂN HÀM ẨN SỬ DỤNG ĐỊNH NGHĨA NGUYÊN HÀM, TÍCH PHÂN

Ý tưởng của dạng toán này xuất phát từ tính chất sau của nguyên hàm:

Trong công thức trên thường ta sẽ biết f'(x) (hàm số bị ẩn ở trong f'(x)) và chưa biết hệ số tự do C nhưng sẽ biết một vài giá trị của f(x). Bài toán sẽ yêu cầu chúng ta tính một vài giá trị khác nào đó của f(x).

Để làm dạng toán này chúng ta có thể sử dụng hai cách sau:

Cách 1: Ta sử dụng định nghĩa và các tính chất của nguyên hàm để xác định f(x)+C. Sau đó sử dụng các giá trị đã biết của f(x) để xác định hệ số tự do C. Tiếp đó ta tính các giá trị cần tìm mà thôi.

Cách 2: Nếu hàm số đã cho khả tích (có tích phân) trên đoạn [a;b] thì ta sử dụng công thức tích phân để tính giá trị.

Lưu ý:

Trong dạng toán này chúng ta cần lưu ý để tránh nhầm lẫn nguyên hàm của hàm số f(x)=1/(ax+b).

Với dạng này ta cần chia hai trường hợp để phá dấu trị tuyệt đối. Và trong hai trường hợp hệ số tự do C có thể khác nhau.

Bài tập minh họa:

Bài 1: Cho hàm số f(x) xác định trên R và có đạo hàm thỏa mãn f'(x)=2x+3 và f(1)=0. Tính f(2).

Lời giải:

Cách 1: Dùng định nghĩa nguyên hàm

Cách 2: Dùng định nghĩa tích phân

Bài 2: Cho hàm số f(x) xác định trên R\{1} thỏa mãn f'(x)=1/(2x-2) và f(0)=1, f(3)=5. Tính S=f(-2)+f(2).

Lời giải:

Cách 1: Dùng định nghĩa nguyên hàm

Cách 2: Dùng định nghĩa tích phân

Ở cách 2 bài này hãy lưu ý ta không thể lấy tích phân trên những đoạn có chứa điểm x=1.

Bài tập Nguyên Hàm Online có giải chi tiết:

Đề thi Online có giải: Đề [9-10 điểm] Nguyên hàm của hàm ẩn hoặc lq đến pt f(x),f’(x),f’’(x)

Bộ đề thi Online các dạng có giải chi tiết: Nguyên Hàm Tích Phân

TÍCH PHÂN HÀM ẨN SỬ DỤNG TÍNH CHẤT CỦA NGUYÊN HÀM, TÍCH PHÂN

Ý tưởng sử dụng tính chất nguyên hàm thì cơ bản xuất phát từ tính chất sau của nguyên hàm (Tích phân cũng có tính chất tương tự):

Ví dụ minh họa:

Lời giải:

Ta thấy cận của tích phân cần tính là từ −1 đến 0. Vì vậy chúng ta cần tách cận của tích phân cần tính sao cho liên quan đến giả thiết.

Chọn được đáp án là A.

TÍCH PHÂN HÀM ẨN SỬ DỤNG PHƯƠNG PHÁP ĐỔI BIẾN SỐ

Nếu trong bài tập trắc nghiệm tích phân mà tích phân cần tính có cận khác với tích phân trong giả thiết. Chúng ta nên nghĩ tới phương pháp đổi biến.

Ví dụ minh họa:

Lời giải:

Ta thấy tích phân cần tính có cận từ 1 tới 6. Trong khi tích phân giả thiết có cận từ 3 tới 13. Vì vậy ở bài này ta sử dụng phương pháp đổi biến. Thong thường chúng ta sẽ đổi biến ở tích phân nào phức tạp hơn.

Chọn được đáp án là D.

Bài tập Nguyên Hàm Online có giải chi tiết:

Đề thi Online có giải: Đề [7-8 điểm] Tích phân đổi biến

TÍCH PHÂN HÀM ẨN SỬ DỤNG PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN

Khi tư duy về tích phân ở mức độ cơ bản thì chúng ta chỉ nên xem xét xem người ta khai thác phần kiến thức nào: Định nghĩa, tính chất, đổi biến hay từng phần. Khi ba phương pháp trên không sử dụng được mà trong tích phân ta lại thấy có 2 hàm số, cận không đổi thì đó có thể là dấu hiệu của tích phân từng phần.

Xem thêm: Tính nhanh tích phân từng phần bằng sơ đồ

Ví dụ minh họa: