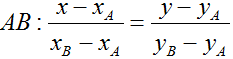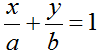Phương trình đường thẳng đi qua 2 điểm lớp 10
Cảm ơn các bạn đã ghé thăm Blog. Bài viết này sẽ hướng dẫn các bạn cách viết phương trình đường thẳng đi qua 2 điểm trong môn Hình học lớp 10.
Content
1. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG ĐI QUA 2 ĐIỂM
Trong mặt phẳng tọa độ, cho điểm và điểm
phân biệt. Khi đó tồn tại duy nhất một đường thẳng đi qua 2 điểm A, B. Để viết phương trình tham số của đường thẳng AB ta xác định yếu tố điểm là A hoặc B. Yếu tố vector chỉ phương chính là
.
Ví dụ:
Trong mặt phẳng Oxy cho điểm A(1;2) và B(3;-1). Viết phương trình tham số của đường thẳng AB.
Giải:
Ta có: là một vector chỉ phương của đường thẳng AB.
Vậy phương trình tham số của đường thẳng AB là:
Các bạn chú ý rằng, cùng một đường thẳng thì phương trình tham số có thể có nhiều dạng khác nhau. Điều đó tùy thuộc vào cách chọn yếu tố điểm và yếu tố véctơ chỉ phương.
2. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG QUA 2 ĐIỂM
Trong mặt phẳng tọa độ, cho điểm và điểm
phân biệt. Để viết phương trình tổng quát của đường thẳng AB ta xác định yếu tố điểm là A hoặc B. Để xác định vectơ pháp tuyến ta tính
. Sau đó bằng cách đổi hoành độ và tung độ cho nhau. Đổi dấu một trong 2 hoành độ hoặc tung độ ta được một vectơ pháp tuyến của đường thẳng AB.
Ví dụ:
Trong mặt phẳng Oxy cho điểm A(1;2) và B(3;-1). Viết phương trình tham số của đường thẳng AB.
Giải:
Ta có .
Suy ra là một vectơ pháp tuyến của đường thẳng AB.
(Chú ý là ở đây ta đã đổi vị trí số 2 và -3 cho nhau. Sau đó đổi dấu số -3)
Vậy phương trình tổng quát của đường thẳng AB là: .
(Chú ý hệ số của x và y lần lượt là hoành độ và tung độ của vectơ pháp tuyến. Còn số 7 là kết quả khi thay tọa độ điểm A vào phần 3x+2y).
3. CÔNG THỨC VIẾT NHANH VÀ CÁC TRƯỜNG HỢP ĐẶC BIỆT
Trong mặt phẳng tọa độ, cho điểm và điểm
phân biệt.
- Nếu hoành độ của A và B khác nhau, đồng thời tung độ của A và B khác nhau. Thì ta có thể dùng công thức sau để viết nhanh phương trình đường thẳng AB:
- Nếu hoành độ điểm A và B giống nhau thì phương trình đường thẳng AB là:
. Đường thẳng khi này song song hoặc trùng với trục Oy.
- Nếu tung độ điểm A và B giống nhau thì phương trình đường thẳng AB là:
.Đường thẳng khi này song song hoặc trùng với trục Ox.
- Nếu A(a;0) và B(0;b) trong đó a.b≠0 thì phương trình AB được viết theo công thức:
- Lấn một chút sang toán 12 nhé. Cụ thể bài toán viết phương trình đường thẳng đi qua 2 điểm cực trị của hàm số bậc 3.
Bài toán: Giả sử hàm số bậc 3 có phương trình y=ax³+bx²+cx+d có 2 điểm cực trị A và B. Viết phương trình đường thẳng AB.
Cách giải:
Ta có: y’=3ax²+2bx+c.
Khi đó hoành độ điểm A và B là nghiệm của phương trình: 3ax²+2bx+c=0.
Chúc các bạn học tập vui vẻ!
Phương Pháp Tọa Độ Oxy -