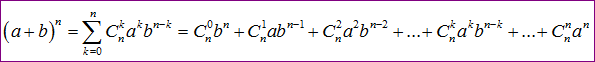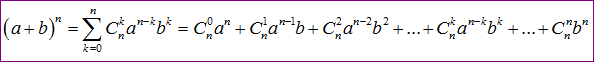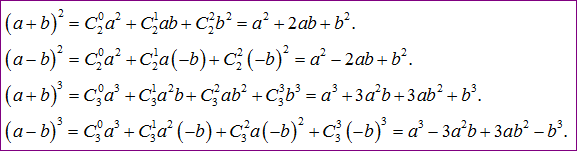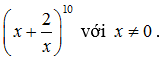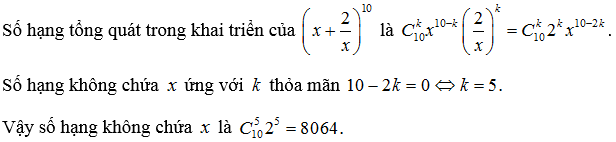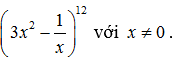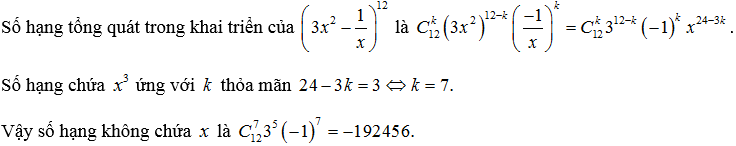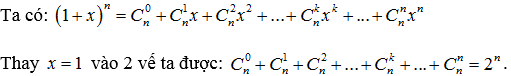Nhị thức Newton: Công thức và một số bài toán
Bài viết dưới đây giới thiệu đến các bạn công thức khai triển nhị thức Newton và một số dạng toán thường gặp. Các bạn theo dõi bài viết để tìm hiểu thêm nhé!
Content
I. CÔNG THỨC NHỊ THỨC NEWTON
Với n là số nguyên dương. Hai số a, b là các số thực. Ta có công thức:
Vì vai trò của a và b như nhau nên hoán đổi vị trí a và b ta có công thức tương đương.
Để dễ nhớ thì các bạn để ý trong mỗi số hạng tổng số mũ của a và b luôn bằng n. Và trong mỗi khai triển có n+1 số hạng.
Áp dụng công thứckhai triển nhị thức newton trên ta có thể dễ dàng khai triển 1 số hằng đẳng thức quen thuộc:
II. CÁC BÀI TOÁN VỀ NHỊ THỨC NEWTON
Dạng 1. Tìm hệ số trong khai triển-Tìm số hạng trong khai triển
Với dạng toán này, các bạn hãy sử dụng số hạng tổng quát (số hạng thứ k+1) của khai triển. Sau đó biến đổi để tách riêng phần biến và phần hệ số. Cuối cùng dựa vào đề bài để xác định chỉ số k. Lưu ý số hạng gồm hệ số+phần biến.
Ví dụ 1:
Tìm số hạng không chứa x trong khai triển của nhị thức
Lời giải:
Ví dụ 2:
Tìm số hạng chứa x³ trong khai triển của nhị thức
Lời giải:
Dạng 2. Một số bài toán liên quan đến khai triển lũy thừa của (1+x)
Đây là một khai triển hay được sử dụng để giải 1 số bài toán liên quan đến nhị thức Νewton.
Ví dụ:
Với n là số nguyên dương, chứng minh rằng:
Lời giải:
Trên đây là công thức khai triển nhị thức Νewton và một số bài toán liên quan. Kiến thức thì vô hạn. Một bài viết ngắn có xíu này chắc chắn chưa thể hiện hết được kiến thức về nhị thức Νewton. Nhưng đó là những kiến thức cơ bản nhất mà các bạn phải hiểu được. Chúc các bạn học giỏi và thành công!
Xem thêm:
Quy tắc đếm: Quy tắc cộng và quy tắc nhân
Tổ hợp xác suất -