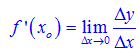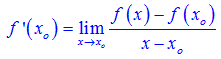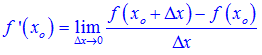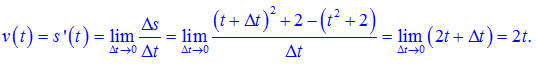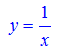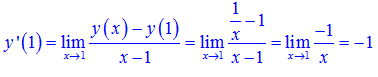Định nghĩa và ý nghĩa của đạo hàm
Cảm ơn các bạn đã ghé thăm Blog. Định nghĩa và ý nghĩa của đạo hàm là gì? Sử dụng công thức để tính đạο hàm thì quá đơn giản rồi phải không nào? Tuy nhiên bài viết này sẽ giới thiệu đến các bạn 3 cách để tính đạo hàm bằng định nghĩa.
1. ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
Định nghĩa: Cho hàm số y=f(x) xác định trên khoảng (a;b) và .
- Khi đó
được gọi là số gia của đối số.
- Còn
được gọi là số gia của hàm số.
Giới hạn nếu tồn tại và hữu hạn thì được gọi là ĐẠO ΗÀM của hàm số y=f(x) tại điểm
.
Và được ký hiệu là .
Tức là
Từ công thức trên ta có thể suy ra các công thức sau:
Hoặc:
Mỗi công thức bên trên đều có điểm thuận tiện riêng. Công thức thứ nhất phù hợp với định nghĩa và ý nghĩa. Công thức thứ 2 phù hợp với việc tính đạo hàm tại một điểm cụ thể. Công thức thứ ba phù hợp với tính đạo hàm tại điểm bất kỳ.
Để hiểu rõ hơn chúng ta xét ví dụ sau:
Ví dụ:
Cho hàm số y=f(x)=x². Tính f'(2).
Lời giải: (Sử dụng công thức thứ 2 nhé!)
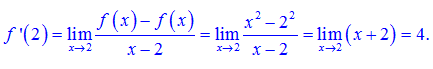
Theo định nghĩa thì đạo hàm thể hiện tỉ lệ mức độ thay đổi của giá trị hàm số so với giá trị của đối số. Do đó đạo hàm của phương trình chuyển động của một vật thể hiện vận tốc tức thời tại một thời điểm nào đó. Đạo hàm của phương trình điện lượng của dòng điện thể hiện cường độ dòng điện tức thời tại một thời điểm nào đó.
Ví dụ:
Một vật chuyển động theo phương trình s(t)=t²+2. Đơn vị của t là giây, đơn vị của s(t) là mét. Tính vận tốc của vật sau khi di chuyển được 10 giây.
Lời giải:
Ta có (sử dụng công thức thứ 3 nhé!)
Do đó vận tốc của vật sau khi di chuyển 10 giây là
2. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
Ý nghĩa: Cho hàm số y=f(x) xác định trên khoảng (a;b) và . Đạo hàm của hàm số tại điểm
chính là hệ số góc của tiếp tuyến tại điểm đó.
Lưu ý: Đối với dạng toán viết phương trình tiếp tuyến ta có 3 dạng như sau:
- Cho hoành độ tiếp điểm.
- Cho tung độ tiếp điểm.
- Cho hệ số góc của tiếp tuyến.
Mỗi dạng toán chúng ta cần phải tìm các đại lượng còn lại để thay vào phương trình tiếp tuyến có dạng
Sau đây ta xét 1 ví dụ cho dạng 1. Các dạng còn lại các bạn tự tìm hiểu nhé:)).
Ví dụ:
Cho hàm số
Viết phương trình tiếp tuyến của hàm số biết hoành độ tiếp điểm là 1.
Lời giải:
Ta có
Giá trị của hàm số tại x=1 là y(1)=1.
Vậy phương trình tiếp tuyến cần tìm là
Chúc các bạn học tập vui vẻ!
Đạo hàm -