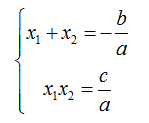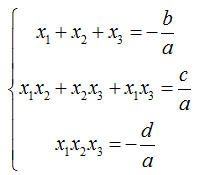Định lí Vi ét trong phương trình và ứng dụng

Bài viết dưới đây giới thiệu đến bạn đọc định lí Vi ét và hướng dẫn các bạn một số ứng dụng của nó trong các bài toán về phương trình.

1. ĐỊNH LÍ VI ÉT (VIÈTE)

Định lý Vi ét  cho phương trình bậc hai:

Thuận:

Cho phương trình bậc hai ax²+bx+c=0 (a≠0) có hai nghiệm . Khi đó:

Đảo:

Nếu S là tổng của hai số thực x và y, P là tích của hai số thực x và y thì x và y là các nghiệm của phương trình X²-SX+P=0 (nếu có).

Định lý Vi-ét cũng đúng đối với phương trình đa thức bậc bất kỳ. Tuy nhiên trong chương trình phổ thông của ta thì thỉnh thoảng chúng ta mới dùng đến định lí vi ét cho phương trình bậc 3 bậc 4 là cao nhất.

Nội dung cụ thể như sau:

Định lí vi-ét cho phương trình bậc 3:

Cho phương trình bậc ba ax³+bx²+cx+d=0 (a≠0) có ba nghiệm . Khi đó:

Định lý Viets đảo đối với phương trình bậc 3 ít được sử dụng trong chương trình cơ bản. Vì vậy phần này các bạn tự tìm hiểu thêm.

2. HỆ THỨC VI ÉT VÀ ỨNG DỤNG

Định lý Vi-et được sử dụng vào việc tìm nghiệm, tính các giá trị biểu thức liên quan đến nghiệm của phương trình đa thức bậc 2 bậc 3. Ngoài ra còn được dùng để nhẩm nghiệm.

Ví dụ 1:

Cho phương trình x²-2x-5=0.  Không giải phương trình tính tổng các nghiệm của phương trình đã cho.

Lời giải:

Nhận xét rằng phương trình có 2 nghiệm trái dấu.

Áp dụng định lý Vi-ét suy ra tổng hai nghiệm của phương trình là 2.

Ví dụ 2:

Biết rằng phương trình x²-2(m+2)x+m+10=0 có hai nghiệm phân biệt a và b. Tìm hệ thức liên hệ giữa a và b không phụ thuộc vào m.

Lời giải:

Áp dụng định lý Vi-et ta có:

a+b=2(m+2) và ab=m+10

Sử dụng phép thế suy ra:

a+b=2(ab-10+2)

Hay rút gọn ta được

a+b-2ab+16=0

Ví dụ 3:

Cho phương trình x²-(2m-1)x+m²+1=0. Tìm m để phương trình có 2 nghiệm phân biệt a và b thỏa mãn

a(1+b)=-1-b

Lời giải:

Ta thấy đẳng thức trong đề bài có “dáng dấp” định lý Vi-ét.

Tuy nhiên để áp dụng được ta phải tìm điều kiện để phương trình đã cho có hai nghiệm phân biệt đã.

Để phương trình có 2 nghiệm phân biệt thì

Δ=(2m-1)²-4(m²+1)>0

Hay rút gọn ta được

m<-3/4.

Từ đẳng thức a(1+b)=-1-b ta rút gọn được

a+b+ab+1=0

Áp dụng định lý Vi-ét ta có:

(2m-1)+m²+1+1=0

Từ đó ta suy ra được:

m=-1 (thỏa mãn Δ>0)

Trên đây là định lý Vi-ét và một số ví dụ vè ứng dụng của nó. Chúc các bạn học tập vui vẻ!