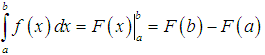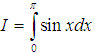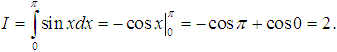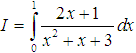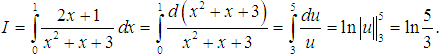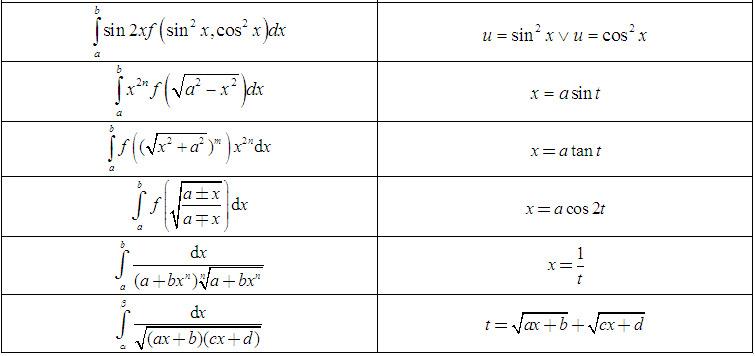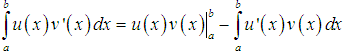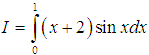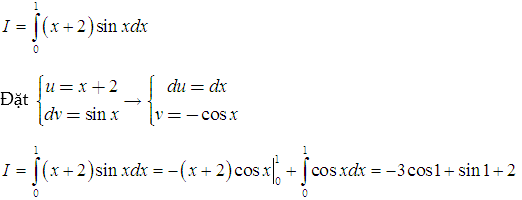Tích phân cơ bản và phương pháp tính tích phân gồm những gì? Bài viết dưới đây sẽ hướng dẫn các công thức tích phân và các phương pháp tính tích phân cốt yếu nhất mà các em học sinh cần nắm được. Các em cùng theo dõi nhé!
TÍCH PHÂN LÀ GÌ
Tích phân có 2 định nghĩa tương đương nhau. Đó là định nghĩa theo công thức Newton-Leibniz và định nghĩa theo giới hạn. Phần định nghĩa theo giới hạn chúng ta sẽ không đề cập ở đây. Các em có thể đọc thêm trong sách giáo khoa.
Định nghĩa tích phân theo công thức Newton-Leibniz “có vẻ” hình thức nhưng dễ vận dụng vào bài tập hơn. Cụ thể:
Cho hàm số y=f(x) xác định và liên tục trên đoạn [a;b] và F(x) là một nguyên hàm nào đó của hàm số y=f(x) trên [a;b]. Khi đó:
TÍNH CHẤT CỦA TÍCH PHÂN CƠ BẢN
Trước tiên chúng ta cần nắm được các tính chất tích phân sau:
PHƯƠNG PHÁP TÍNH TÍCH PHÂN
Các cách tính tính tích phân cơ bản gồm 3 phương pháp:
Phương pháp tính trực tiếp: Đây là cách tính tích phân mà ta sử dụng bảng nguyên hàm để thay trực tiếp vào công thức Newton-Leibniz.
Ví dụ minh họa (Tự luận):
Tính tích phân sau:
Lời giải:
Vì nguyên hàm của sinx là −cosx nên:
Phương pháp giải toán tích phân bằng đổi biến:
Một trong các phương pháp giải tích phân là sử dụng công thức đổi biến số:
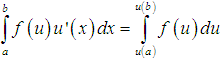
Công thức tính tích phân bằng đổi biến
Ví dụ minh họa (Tự luận):
Tính tích phân sau:
Lời giải:
Ta nhận thấy mẫu số đạo hàm được tử số. Đây là dấu hiệu của phương pháp đổi biến. Áp dụng công thức đổi biến ta có:
Các dạng tích phân đổi biến:
Dưới đây là tổng hợp các dạng tích phân và cách giải (cách đổi biến) thường gặp:
Cách giải toán tích phân bằng phương pháp tích phân từng phần:
Các dạng bài tập tích phân cần sử dụng tích phân từng phần khi hàm số dưới dấu tích phân thuộc một trong các loại: Đa thức-lượng giác; Đa thức-mũ; Logarit-đa thức; Mũ-lượng giác. Và tích phân đó không sử dụng được hoặc khó sử dụng phương pháp đổi biến.
Công thức tích phân từng phần:
Ví dụ minh họa (Tự luận):
Tính tích phân
Lời giải:
Chhúng ta đặt u(x) theo thứ tự ưu tiên: ” Nhất lô nhì đa tam lượng tứ mũ”.
Chúc các em thành công!
Xem thêm:
Tính nhanh tích phân từng phần bằng sơ đồ
Ứng dụng tích phân trong hình học
Tích phân hàm ẩn – Lý thuyết và bài tập minh họa