Tập hợp con và số tập hợp con của tập hợp
Cảm ơn các bạn đã ghé quan blog. Bài viết dưới sẽ giới thiệu đến các bạn khái niệm tập hợp con của một tập hợp. Đồng thời giới thiệu một vài kiến thức liên quan.
TẬP HỢP CON LÀ GÌ
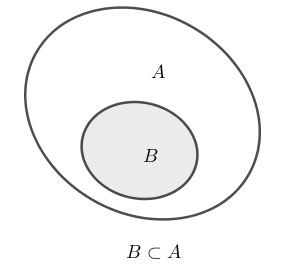
Cho A là một tập hợp bất kỳ. Tập hợp B được gọi là tập con của tập A nếu mọi phần tử của tập B đều là phần tử của tập A. Khi đó kí hiệu tập hợp con sẽ là B⊂A (hoặc B⊆A).
Khi đó tập con có thể biểu diễn bằng biểu đồ Ven như sau:
Như vậy theo định nghĩa trên thì tập bất kỳ luôn có 2 tập con là tập rỗng (ký hiệu ∅) và chính nó (là tập A).
Ví dụ về tập con:
Chẳng hạn A là tập hợp một số loại hoa quả A={cam, xoài, mít, mận}. Ta có thể kể ra một số tập con của tập A như sau: {cam}, {cam, xoài}, {cam, mít, mận},…
Rõ ràng khi số phần tử của một tập càng nhiều lên thì số tập con cũng nhiều lên. Vậy ta có thể đếm được số tập con của một tập không? Phần tiếp sau đây sẽ trả lời câu hỏi đó.
CÁCH TÍNH SỐ TẬP HỢP CON
Tính chất 1: Cho tập hợp A có n phần tử. Số tập con của A được tính theo công thức: 
.
Chẳng hạn tập hợp A={a, b, c}. Khi đó tập A sẽ có 2³=8 tập con. Cụ thể các tập con đó có thể liệt kê gồm:
ø, {a}, {b}, {c}, {a, b}, {b, c}, {a, c} và {a, b, c}.
Ta có thể chứng minh tính chất trên bằng quy nạp như sau:
- Với n=0, tập rỗng có 2°=1 tập con. Đúng.
- Với n=1, có 2¹=2 tập con là rỗng và chính nó. Đúng.
- Giả sử với n=k (k≥1), tập có
tập con. Ta xét tập có k+1 phần tử. Ta chọn ra k phần tử, từ đó tạo thành tập con theo giả thiết quy nạp. Ngoài ra ta bổ sung phần tử thứ k+1 vào các tập con đó ta sẽ có thêm tập con mới nữa. Vì vậy ta có tất cả tập con. - Vậy tính chất đã được chứng minh.
tập con. Ta xét tập có k+1 phần tử. Ta chọn ra k phần tử, từ đó tạo thành 
tập con.Tính chất 2: Cho tập hợp A có n phần tử. Số tập con có k phần tử của tập A là 
.
Thực vậy, theo định nghĩa tổ hợp thì mỗi tổ hợp là một tập con có k phần tử của tập có n phần tử. Vì vậy số tập con có k phần tử là số tổ hợp chập k của n.
Ví dụ: Cho tập A có 5 phần tử. Tính số tập hợp con của A có 3 phần tử.
Lời giải: Theo tính chất 2 thì số tập con là 
.
Trên đây là khái niệm tập con và một số tính chất liên quan. Chúc các bạn học giỏi và thành công!
Xem thêm: Mệnh đề và mệnh đề chứa biến
Mệnh đề tập hợp -