Hệ thức lượng trong tam giác và giải tam giác
Bài viết dưới đây tổng hợp lại lý thuyết phần hệ thức lượng trong tam giác. Nhìn chung thì đây là một phần kiến thức xuyên suốt toán THPT. Đến tận những lớp cuối cấp thì hệ thức lượng của tam giác vẫn được khai thác để giải toán. Vậy những công thức nào chúng ta cần phải nhớ. Tất cả sẽ có bên dưới đây.
Content
1. QUY ƯỚC CHUNG VỀ KÝ HIỆU
Để tiện cho việc tính toán cũng như nhớ công thức. Chúng ta có quy ước chung về việc ký hiệu độ dài và các đại lượng trong một tam giác như sau:
Trong tam giác ABC thì:
- Độ dài các cạnh đối diện với đỉnh A, B, C lần lượt được ký hiệu là a, b, c. Nghĩa là AB=c, BC=a, CA=b.
- Độ dài các đường cao xuất phất từ các đỉnh A, B, C lần lượt ký hiệu là
.
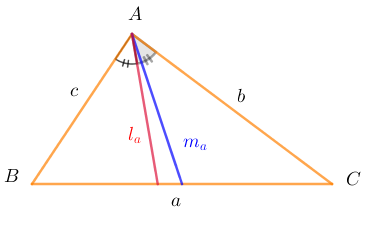
- Độ dài các đường trung tuyến xuất phất từ các đỉnh A, B, C lần lượt ký hiệu là
.
- Độ dài các đường phân giác trong xuất phất từ các đỉnh A, B, C lần lượt ký hiệu là
.
- Diện tích tam giác ký hiệu là S. Bán kính đường tròn nội tiếp ký hiệu là r. Bán kính đường tròn ngoại tiếp ký hiệu là R. Nửa chu vi tam giác ký hiệu là p.
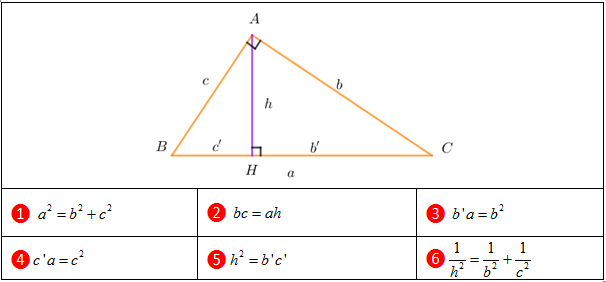
2. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Các hệ thức lượng của tam giác vuông là các trường hợp đặc biệt của các hệ thức lượng trong tam giác thường. Tất cả các hệ thức lượng của tam giác vuông được liệt kê trong bảng sau:
3. HỆ THỨC LƯỢNG TRONG TAM GIÁC – ĐỊNH LÝ COSIN
Định lý cosin trong tam giác có thể được phát biểu thành lời như sau:
Trong một tam giác bất kỳ, bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại trừ đi 2 lần tích 2 cạnh đó với cosin của góc xen giữa.
Người ta cũng rút cosin của góc từ công thức của định lý cosin và dùng nó như một hệ quả để tính góc.
Ta có thể nhận xét rằng, trong giải tam giác người ta thường sử dụng định lý cosin khi yếu tố cạnh nhiều hơn yếu tố góc.
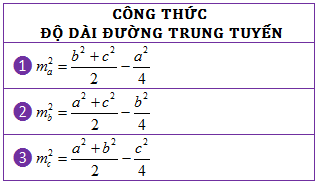
Một hệ quả quan trọng khác của định lý cosin là công thức tính độ dài đường trung tuyến:
 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC – ĐỊNH LÝ SIN
4. HỆ THỨC LƯỢNG TRONG TAM GIÁC – ĐỊNH LÝ SIN
Nói thêm rằng, tên của hai định lý cosin và sin không phải là tên của nhà toán học nào cả nhé. Đơn giản bởi trong công thức của mỗi định lý có giá trị lượng giác sin và cosin mà thôi. Cụ thể định lý sin trong tam giác như sau:
Trong một tam giác bất kỳ, tỉ số giữa độ dài một cạnh và sin của góc đối diện bằng nhau và bằng 2 lần bán kính đường tròn ngoại tiếp tam giác đó.
Trong giải tam giác, người ta thường sử dụng định lý sin khi biết nhiều yếu tố góc hơn yếu tố cạnh.
5. CÔNG THỨC TÍNH DIỆN TÍCH TAM GIÁC
Nhắc đến các hệ thức lượng tam giác và giải tam giác thì không thể thiếu công thức tính diện tích tam giác được.
Công thức số 5 là một công thức nổi tiếng mang tên Hê-rông. Tuy nhiên vì khá cồng kềnh. Nên đây cũng là một công thức nên hạn chế dùng trong giải toán phổ thông.
Trên đây là các công thức hệ thức lượng tam giác. Chúc các em học tập vui vẻ và thành công!
Tích vô hướng -