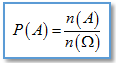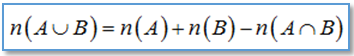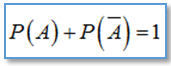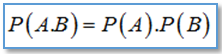Tính xác suất theo định nghĩa cổ điển như thế nào?
Chúng ta có nhiều hơn 1 định nghĩa về xác suất. Chẳng hạn như định nghãi cổ điển về xác suất, định nghĩa thống kê về xác suất, định nghĩa hình học về xác suất. Bài viết dưới đây xin giới thiệ đến các bạn cách tính xác suất theo định nghĩa cổ điển về xác suất. Các bạn theo dõi bài viết để tìm hiểu nhé.
Content
I. ĐỊNH NGHĨA CỔ ĐIỂN VỀ XÁC SUẤT
Một phép thử ngẫu nhiên là một phép thử mà ở đó ta chưa biết kết quả nhưng lại biết được hết các khả năng có thể xảy ra của phép thử. Tất cả các khả năng của phép thử đó được gọi là không gian mẫu. Không gian mẫu được ký hiệu là Ω.
Một biến cố của phép thử ngẫu nhiên là một tập con của không gian mẫu.
Tập con rỗng của Ω gọi là biến cố không thể.
Tập con Ω của Ω gọi là biến cố chắc chắn.
Hai biến cố không có phần chung nhau gọi là hai biến cố xung khắc.
Hai biến cố xung khắc và hợp với nhau bằng Ω gọi là 2 biến cố đối nhau.
Xác suất của biến cố A theo định nghĩa cổ điển đặc trưng cho khả năng xảy ra của biến cố đó thấp hay cao. Công thức tính xác suất là
Trong đó n(A) là số phần tử của biến cố A. n(Ω) là số phần tử không gian mẫu.
Ví dụ:
Gieo ngẫu nhiên 1 con súc sắc cân đối và đồng chất. Xác suất để mặt có số chấm chẵn xuất hiện là bao nhiêu?
Lời giải:
Không gian mẫu là Ω={1;2;3;4;5;6}.
Số phần tử không gian mẫu là n(Ω)=6.
Gọi A là biến cố mặt có số chấm chẵn xuất hiện.
A={2;4;6} nên số phần tử của A là n(A)=3.
Vậy xác suất để mặt có số chấm chẵn xuất hiện là P(A)=n(A)/n(Ω)=1/2.
II. CÁC CÔNG THỨC TÍNH XÁC SUẤT
Như vậy theo định nghĩa bên trên, cách tính xác suất là tính số phần tử của không gian mẫu và số phần tử của biến cố sau đó lập tỉ số.
Ngoài ra chúng ta cũng có thể tính thông qua một số công thức sau:
-
Công thức đếm số phần tử của hợp 2 tập hợp:
Ví dụ:
Trong lớp 12A1 có 33 bạn học sinh. Trong đó có 12 bạn học lực giỏi môn Toán, 15 bạn học lực giỏi môn Văn, 21 bạn học lực giỏi ít nhất một trong hai môn Toán, Văn. Chọn ngẫu nhiên từ lớp 1 bạn để tham dự đại hội Đoàn trường. Xác suất để bạn học sinh được chọn giỏi cả 2 môn Toán và Văn là bao nhiêu?
Lời giải:
Áp dụng công thức trên ta có số học sinh giỏi cả Toán và Văn là: 12+15-21=6.
Vậy xác suất cần tìm là: 6/33=2/11.
-
Tính xác suất thông qua biến cố đối
Trong một số bài toán mà xuất hiện các từ như ít nhất, hơn… thì ta có thể suy nghĩ đến việc tìm xác suất thông qua biến cố đối.
Công thức xác suất biến cố đối:
Ví dụ:
Trong một hộp có 5 viên bi đỏ và 11 viên bi vàng. Lấy ra ngẫu nhiên 5 viên bi. Xác suất để trong 5 viên bi lấy ra có ít nhất 1 viên bi đỏ là bao nhiểu?
Lời giải:
Nếu không tính theo biến cố đối ta có thể thấy cần chia rất nhiều trường hợp để đếm. Chẳng hạn như 1 đỏ 4 xanh, 2 đỏ 3 xanh, 3 đỏ 2 xanh… Nhưng nếu sử dụng biến cố đối để tính thì bài toán đơn giản hơn rất nhiều.
-
Công thức nhân xác suất:
Hai biến cố độc lập nếu như việc xảy ra của biến cố này không ảnh hưởng đến xác suất của biến cố kia. Biến cố độc lập có một định nghĩa tương đương bằng công thức.
Ví dụ:
Ba xạ thủ cùng bắn vào 1 bia với xác xuất trúng đích lần lượt là 0,7; 0,6; 0,8. Xác suất để ba xạ thủ cùng bắn trúng đích là bao nhiêu?
Lời giải:
Việc bắn trúng đích của mỗi xạ thủ không ảnh hưởng đến việc trúng đích của xạ thủ khác. Vậy xác suất cần tìm là
0,7×0,6×0,8=0,336.
Trên đây là một số kiến thức về xác suất ở bậc THPT mà toanthaydinh.com giới thiệu đến các bạn. Chúc các bạn học giỏi và thành công!
Xem thêm:
Hoán vị, chỉnh hợp và tổ hợp: Công thức và các dạng chi tiết
Tổ hợp xác suất -